Neural State as Solution: How NPDOA is Revolutionizing Drug Discovery Optimization

Amelia Ward Dec 02, 2025 480

This article explores the Neural Population Dynamics Optimization Algorithm (NPDOA), a novel brain-inspired meta-heuristic that represents potential solutions as neural states.

Neural State as Solution: How NPDOA is Revolutionizing Drug Discovery Optimization

Abstract

This article explores the Neural Population Dynamics Optimization Algorithm (NPDOA), a novel brain-inspired meta-heuristic that represents potential solutions as neural states. Tailored for researchers and drug development professionals, we dissect NPDOA's core mechanics—its three dynamic strategies of attractor trending, coupling disturbance, and information projection. The content covers its foundational theory, methodological application in complex drug discovery tasks like molecule generation and target prioritization, strategies for troubleshooting common optimization challenges, and a comparative analysis with other state-of-the-art algorithms. By validating its performance against benchmarks and real-world problems, this article provides a comprehensive resource for understanding and applying this cutting-edge bio-inspired optimization tool.

The Brain as an Optimizer: Unpacking the Foundations of NPDOA and Neural State Representation

Brain-inspired meta-heuristic algorithms represent a frontier in computational intelligence, translating the brain's principles for solving complex optimization problems in biomedicine. Unlike traditional algorithms inspired by swarm behaviors or evolution, these methods directly model the information processing and decision-making capabilities of neural systems [1]. A cornerstone concept in this field is the neural state as a solution representation, a principle central to the Neural Population Dynamics Optimization Algorithm (NPDOA), where the dynamic state of a neural population encodes a potential solution to an optimization problem [1]. This paradigm leverages the brain's efficiency in navigating high-dimensional problem spaces, offering enhanced capabilities for exploration and exploitation in biomedical applications ranging from medical image analysis and drug discovery to personalized treatment planning [2] [3] [4]. This guide provides an in-depth technical examination of these algorithms, their core mechanisms, and their practical implementation in biomedical research.

Core Principles and Algorithmic Frameworks

The operational core of brain-inspired meta-heuristics lies in translating high-level neural processes into mathematical optimization strategies.

The Neural State as a Solution Representation

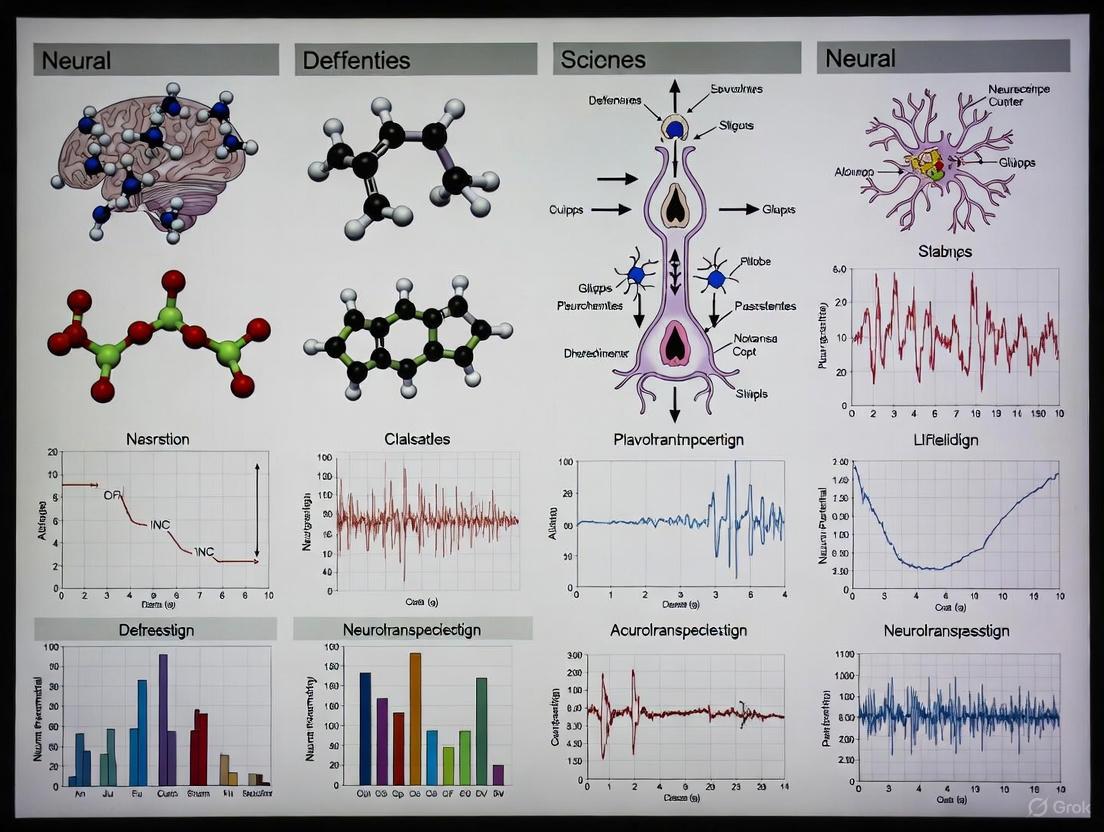
In the NPDOA framework, a candidate solution to an optimization problem is represented by the neural state of a population of neurons [1]. Each decision variable in the D-dimensional solution vector ( x = (x1, x2, ..., x_D) ) corresponds to a neuron, and the value of that variable represents the neuron's firing rate [1]. The algorithm simulates the interactive dynamics of multiple such neural populations to evolve these solutions toward an optimum.

Key Dynamics and Search Strategies

NPDOA implements three brain-inspired strategies to balance global search (exploration) and local refinement (exploitation) [1]:

  • Attractor Trending Strategy: This drives the neural states of populations towards stable attractors, which represent favorable decisions, thereby ensuring exploitation capability.
  • Coupling Disturbance Strategy: This disrupts the convergence of neural populations towards their attractors by introducing interference from other populations, thus improving exploration and helping to escape local optima.
  • Information Projection Strategy: This controls communication between neural populations, enabling a dynamic transition from exploration to exploitation over the course of the optimization.

Other advanced frameworks, such as MARBLE (MAnifold Representation Basis LEarning), take a different approach by using differential geometry to characterize the dynamics of neural populations. MARBLE decomposes neural dynamics into local flow fields, creating a statistical representation that is highly interpretable and can be used to compare dynamics across different systems or conditions [5].

The following diagram illustrates the typical workflow of a brain-inspired optimization algorithm like NPDOA, showing the interaction between its core components.

NPDOA NPDOA Core Workflow Start Initialize Neural Populations Evaluate Evaluate Neural States (Fitness Calculation) Start->Evaluate Attractor Attractor Trending (Exploitation) Disturbance Coupling Disturbance (Exploration) Attractor->Disturbance Projection Information Projection (Balancing) Disturbance->Projection Projection->Evaluate Update States Evaluate->Attractor Check Convergence Met? Evaluate->Check Check->Attractor No End Output Optimal Neural State Check->End Yes

Applications in Biomedicine and Performance Analysis

Brain-inspired meta-heuristics have demonstrated significant impact across various biomedical domains, often outperforming established nature-inspired algorithms.

Table 1: Performance of Bio-Inspired Algorithms in Medical Image Segmentation (Based on [2])

Algorithm Primary Application Key Metric (DSC) Key Metric (JI) Notable Advantage
PSO Hyperparameter Tuning ~0.91 ~0.84 Rapid convergence in preprocessing optimization
Genetic Algorithm (GA) Architecture Search ~0.89 ~0.82 Effective for small-sample scenarios
Grey Wolf Optimizer (GWO) Attention Mechanism Optimization ~0.90 ~0.83 Balanced exploration/exploitation
Whale Optimization Algorithm (WOA) Multimodal Data Fusion ~0.89 ~0.81 Robustness to local optima
Hybrid CJHBA/BioSwarmNet End-to-End Pipeline Optimization >0.92 >0.86 Superior accuracy and robustness

Table 2: Performance of Brain-Inspired Optimizers in Medical Data Analysis (Based on [3])

Algorithm Dataset Accuracy (%) F1-Score (%) Precision (%)
NeuroEvolve MIMIC-III 94.1 91.3 92.5
NeuroEvolve Diabetes 92.5 90.1 91.8
NeuroEvolve Lung Cancer 95.0 93.2 94.1
Hybrid Whale Optimization (HyWOA) MIMIC-III 89.6 85.1 86.9
Hybrid GWO (HyGWO) MIMIC-III 88.3 83.4 84.7

Beyond pattern recognition, these algorithms are revolutionizing macroscopic brain modeling. A dynamics-aware quantization framework allows coarse-grained brain models to run on low-precision, high-efficiency brain-inspired computing chips (e.g., Tianjic). This has achieved a 75–424 times acceleration over CPU-based simulations, reducing model inversion time for fitting empirical neuroimaging data to just 0.7–13.3 minutes, paving the way for clinical applications in understanding brain disorders [6]. In neuroradiology, frameworks integrating brain-inspired computation with big-data analytics (BDA-D) have achieved a diagnostic accuracy of 97.18%, a processing speed increase of 95.42%, and high reliability (94.96%), significantly reducing inter-observer variability [4].

Experimental Protocols and Methodologies

Implementing brain-inspired meta-heuristics requires careful experimental design. Below is a protocol for applying the NPDOA framework to a biomedical optimization problem.

Protocol: Hyperparameter Optimization for a Deep Learning Model in Medical Image Analysis

This protocol details the use of NPDOA to optimize the hyperparameters of a convolutional neural network for a task such as brain tumor segmentation on MRI data [2] [1].

  • Objective: To find the optimal set of hyperparameters ( H = { \text{learning rate}, \text{batch size}, \text{dropout rate}, \text{number of filters} } ) that maximizes the Dice Similarity Coefficient (DSC) of a segmentation model.

  • Step 1: Problem Formulation and NPDOA Setup

    • Solution Representation: Define a neural state (solution vector) where each variable corresponds to one hyperparameter. For example, a 4-dimensional state ( x = (x1, x2, x3, x4) ).
    • Search Space: Define feasible bounds for each variable (e.g., learning rate ( x_1 \in [1e-5, 1e-2] )).
    • Fitness Function: ( f(x) = \text{DSC}_{\text{validation}} ). The goal is to maximize ( f(x) ).
    • Algorithm Parameters: Initialize NPDOA parameters (e.g., number of neural populations, parameters governing the three core strategies).

  • Step 2: Iterative Optimization Loop

    • Initialization: Randomly generate the initial neural states (hyperparameter sets) for all populations within the defined search space.
    • Fitness Evaluation: For each neural state, instantiate and train the segmentation model with the corresponding hyperparameters. Evaluate the model on the validation set to obtain the DSC, which is the fitness value.
    • Strategy Application:
      • Apply the Attractor Trending Strategy to guide populations towards the current best hyperparameter sets.
      • Apply the Coupling Disturbance Strategy to perturb hyperparameters and explore new regions of the search space.
      • Apply the Information Projection Strategy to balance the influence of the above two strategies.
    • Termination Check: Repeat steps 2-3 until a stopping criterion is met (e.g., maximum iterations, or fitness convergence).

  • Step 3: Validation

    • The best-performing neural state (hyperparameter set) identified by NPDOA is used to train a final model on the combined training and validation data.
    • The model's performance is ultimately reported on a held-out test set.

This workflow for model optimization is visualized below.

HyperparameterOptimization Hyperparameter Optimization Workflow ProblemDef Define Hyperparameters and Search Space NPDOA_Init Initialize NPDOA Neural Populations ProblemDef->NPDOA_Init Eval Evaluate Hyperparameters (Train & Validate Model) NPDOA_Init->Eval Update Update Neural States via NPDOA Strategies Eval->Update Check Stopping Met? Eval->Check Update->Eval Next Iteration Check->Eval No FinalModel Train Final Model with Best Hyperparameters Check->FinalModel Yes

Successful research and application in this field rely on a combination of datasets, software tools, and computing resources.

Table 3: Key Resources for Brain-Inspired Metaheuristic Research

Resource Name Type Primary Function Example in Use
Multimodal Neuroimaging Datasets Data Provide empirical data for model fitting/validation. Includes T1, T1CE, T2, FLAIR MRI, fMRI, dMRI [2] [7]. Used to validate coarse-grained brain models and segmentation algorithms [6] [7].
Medical Data Repositories Data Benchmark medical datasets for predictive model training. MIMIC-III, Diabetes Prediction, and Lung Cancer datasets used to validate NeuroEvolve [3].
Brain-Inspired Computing Hardware Hardware Specialized architectures (e.g., Tianjic, Loihi) for low-precision, high-parallelism simulation [6]. Accelerates macroscopic brain model inversion by orders of magnitude [6].
Optimization & Simulation Software Software Libraries for implementing and testing algorithms (e.g., PlatEMO). PlatEMO v4.1 used for experimental studies of NPDOA [1].
Geometric Deep Learning Frameworks Software Tools for implementing advanced concepts like manifold learning. Used by the MARBLE framework for unsupervised representation of neural dynamics [5].

The Neural Population Dynamics Optimization Algorithm (NPDOA) represents a paradigm shift in meta-heuristic optimization by translating the computational principles of brain neuroscience into an algorithmic framework. At its core, NPDOA treats the neural state of a population as a potential solution to an optimization problem, where each decision variable corresponds to a neuron's firing rate within that population [1]. This conceptual mapping establishes a biological plausibility to the optimization process, mirroring how interconnected neural populations in the brain perform sensory, cognitive, and motor calculations to arrive at optimal decisions [1]. The fundamental thesis of NPDOA research posits that the brain's remarkable efficiency in processing diverse information types and contexts can be distilled into computational strategies that balance two competing objectives: thoroughly searching promising regions of the solution space (exploitation) while maintaining the flexibility to discover new potential solutions (exploration) [1].

The NPDOA framework is grounded in population doctrine from theoretical neuroscience, which provides a mathematical foundation for modeling the collective behavior of neural ensembles [1]. Within this framework, the algorithm simulates the activities of multiple interconnected neural populations during cognitive decision-making processes, with neural states evolving according to mathematically defined neural population dynamics [1]. This approach distinguishes itself from other meta-heuristic algorithms by directly embedding neuroscientific principles into its operational mechanics, positioning it as the first swarm intelligence optimization algorithm that systematically utilizes human brain activity patterns for computational problem-solving [1].

Theoretical Foundation of NPDOA

The theoretical underpinnings of NPDOA rest on three strategically designed mechanisms that govern the evolution of neural states toward optimal solutions. Each mechanism corresponds to a specific aspect of neural population behavior observed in neuroscientific studies, creating a comprehensive framework for navigating complex solution spaces.

The attractor trending strategy implements the exploitation capability of NPDOA by driving neural populations toward stable neural states associated with favorable decisions [1]. In computational neuroscience, attractor states represent preferred patterns of neural activity that correspond to specific decisions or memory representations. Within the NPDOA framework, these attractors function as local optima in the solution space, pulling nearby neural states toward them through mathematical operations that simulate the brain's tendency to settle into stable decision states. This mechanism ensures that once promising regions of the solution space are identified, the algorithm can thoroughly search their vicinity for the optimal solution, mirroring how neural circuits converge on decisions through competitive dynamics between neuronal populations.

Coupling Disturbance Strategy

Counterbalancing the convergent nature of attractor trending, the coupling disturbance strategy introduces controlled disruptions that deviate neural populations from their current trajectories toward attractors [1]. This mechanism implements the exploration capability of NPDOA by simulating the cross-coupling interactions between different neural populations that prevent premature convergence to suboptimal decisions. Mathematically, this strategy introduces perturbations through coupling terms that connect distinct neural populations, creating transient deviations that enable the exploration of alternative solutions beyond immediate attractor basins. This approach mirrors the neurobiological phenomenon where neural circuits maintain flexibility through inhibitory interactions and competitive dynamics, preventing pathological fixation on single patterns and enabling adaptive switching between behavioral strategies based on changing environmental contingencies.

Information Projection Strategy

Serving as the regulatory mechanism between exploitation and exploration, the information projection strategy controls communication between neural populations to enable a seamless transition from exploration to exploitation phases [1]. This strategy mathematically modulates the influence of the attractor trending and coupling disturbance strategies on neural states, creating a dynamic balance that evolves throughout the optimization process. In early stages, information projection may prioritize coupling disturbance to facilitate broad exploration of the solution space, while gradually shifting toward attractor trending as the algorithm identifies promising regions. This adaptive regulation mirrors how neural systems employ gating mechanisms—often through neuromodulatory influences—to control information flow between brain regions based on task demands and behavioral context.

Table 1: Core Strategies in Neural Population Dynamics Optimization Algorithm

Strategy Computational Function Neuroscientific Basis Optimization Role
Attractor Trending Drives neural populations toward optimal decisions Stable neural states associated with favorable decisions Ensures exploitation capability
Coupling Disturbance Deviates neural populations from attractors via coupling Cross-population neural interactions that prevent fixation Improves exploration ability
Information Projection Controls communication between neural populations Neuromodulatory gating of information flow between brain regions Regulates transition from exploration to exploitation

Experimental Methodologies for Studying Neural Population Dynamics

Research into neural population dynamics employs sophisticated experimental platforms that enable simultaneous recording and perturbation of neural circuits. These methodologies provide the empirical foundation for understanding how collective neural activity gives rise to cognitive operations like decision-making.

Two-Photon Holographic Optogenetics with Calcium Imaging

Cutting-edge experiments in neural population dynamics combine two-photon holographic optogenetics with simultaneous two-photon calcium imaging to establish causal relationships between neural activity and cognitive functions [8]. This integrated approach enables researchers to precisely stimulate experimenter-specified groups of individual neurons while measuring resulting activity across the entire neural population. In typical experimental protocols, neural population activity is recorded at high temporal resolutions (e.g., 20Hz) across fields of view containing hundreds of neurons [8]. Each photostimulation trial delivers a precisely timed photostimulus (e.g., 150ms duration) targeting specific groups of 10-20 neurons, followed by an extended response period (e.g., 600ms) to observe the propagation of neural dynamics through the circuit [8]. Through repeated trials with different photostimulation patterns, researchers can build comprehensive maps of causal influences within neural populations, providing rich datasets for inferring the underlying dynamical principles that govern population-level computations.

MARBLE Framework for Neural Dynamics Representation

The MAnifold Representation Basis LEarning (MARBLE) framework provides an advanced methodological approach for extracting interpretable representations from neural population dynamics using geometric deep learning [9]. This technique addresses the fundamental challenge that neural dynamics typically evolve on low-dimensional manifolds embedded within the high-dimensional space of neural activities. The MARBLE workflow begins with representing local dynamical flow fields anchored to neural state point clouds, approximating the underlying manifold through proximity graphs [9]. The framework then employs a specialized geometric deep learning architecture consisting of: (1) gradient filter layers that provide p-th order approximations of local flow fields; (2) inner product features with learnable linear transformations that ensure embedding invariance; and (3) a multilayer perceptron that outputs latent representations [9]. This unsupervised approach discovers emergent low-dimensional latent representations that parametrize high-dimensional neural dynamics during cognitive operations like gain modulation and decision-making, enabling robust comparison of neural computations across different networks and animals without requiring behavioral supervision [9].

Table 2: Key Experimental Parameters in Neural Population Dynamics Research

Experimental Parameter Typical Setting Functional Significance
Recording Frequency 20Hz [8] Balances temporal resolution with computational constraints
Field of View 1mm×1mm [8] Captures hundreds of neurons within a local circuit
Neurons Recorded 500-700 [8] Provides sufficient population statistics for dynamics identification
Photostimulus Duration 150ms [8] Sufficient to evoke neural responses without causing adaptation
Response Period 600ms [8] Allows observation of dynamics propagation through the network
Photostimulation Group Size 10-20 neurons [8] Large enough to perturb network dynamics, small enough for specificity
Unique Stimulation Groups 100 per experiment [8] Provides comprehensive sampling of network interactions

Quantitative Analysis of Neural Population Dynamics

Rigorous quantitative analysis is essential for extracting meaningful insights from neural population data and validating the performance of algorithms like NPDOA. This section details key analytical frameworks and presents empirical results that demonstrate the effectiveness of neural population dynamics approaches.

Low-Rank Autoregressive Modeling

Neural population dynamics frequently exhibit low-dimensional structure, residing in subspaces of significantly lower dimension than the total number of recorded neurons [8]. This observation has led to the development of low-rank autoregressive models that efficiently capture the essential features of population dynamics while reducing computational complexity. These models parameterize the dynamics using diagonal plus low-rank matrices, where the diagonal components account for neuron-specific autocorrelations and reliable responses to direct photostimulation, while the low-rank components capture shared population-level dynamics [8]. Formally, these models are described by the equation:

[ x{t+1} = \sum{s=0}^{k-1} (D{As} + U{As}V{As}^\top) x{t-s} + (D{Bs} + U{Bs}V{Bs}^\top) u{t-s} + v ]

where (D) represents diagonal matrices, (U) and (V) are low-rank factors, and (v) accounts for baseline neural activity [8]. This parameterization dramatically reduces the number of free parameters while maintaining expressive power to capture population-wide dynamical features, enabling more efficient estimation from limited experimental data.

Active Learning for Efficient Dynamics Identification

Recent advances have introduced active learning approaches that strategically select photostimulation patterns to maximize information gain about neural population dynamics. These methods address the fundamental constraint that photostimulation experiments are time-intensive, making exhaustive testing of all possible stimulation patterns impractical [8]. Active learning procedures leverage low-rank structure to identify which photostimulation patterns will most efficiently reduce uncertainty about the underlying dynamics. This approach represents a significant departure from traditional passive experimental designs where stimulation patterns are predetermined, instead adapting the experimental protocol based on accumulating data [8]. Empirical results demonstrate that this active approach can achieve up to a two-fold reduction in the amount of data required to reach a given predictive power compared to passive baselines [8], substantially accelerating the identification of neural population dynamics.

Performance Benchmarking

The NPDOA algorithm has undergone rigorous evaluation against established meta-heuristic algorithms across diverse benchmark and practical engineering problems [1]. Performance comparisons include compression spring design, cantilever beam design, pressure vessel design, and welded beam design problems [1]. Results demonstrate that NPDOA offers distinct advantages when addressing many single-objective optimization problems, particularly in scenarios requiring careful balance between exploration and exploitation [1]. The algorithm's brain-inspired architecture enables it to avoid common pitfalls of other methods, such as premature convergence to local optima (a limitation of many evolutionary algorithms) and excessive computational complexity in high-dimensional spaces (a challenge for some swarm intelligence algorithms) [1].

Visualization Frameworks for Neural Dynamics

G NeuralStates Neural States (Population Activity) ProximityGraph Construct Proximity Graph NeuralStates->ProximityGraph TangentSpaces Define Tangent Spaces ProximityGraph->TangentSpaces LocalFlowFields Extract Local Flow Fields (LFFs) TangentSpaces->LocalFlowFields GeometricDL Geometric Deep Learning LocalFlowFields->GeometricDL LatentVectors Latent Representation Z = (z₁, ..., zₙ) GeometricDL->LatentVectors DynamicsDistance Compute Dynamics Distance LatentVectors->DynamicsDistance

MARBLE Framework Workflow

Effective visualization of neural population dynamics is essential for interpreting complex dynamical patterns and communicating scientific insights. The MARBLE framework provides a comprehensive approach for creating interpretable representations of neural dynamics through geometric deep learning [9].

Manifold Representation and Local Flow Fields

The MARBLE framework begins by representing neural population activity as a set of d-dimensional time series {x(t; c)} under different experimental conditions c [9]. Rather than treating individual neural states in isolation, MARBLE characterizes the local dynamical flow fields around each state by first approximating the underlying neural manifold through proximity graphs [9]. This graph-based representation enables the definition of tangent spaces around each neural state and establishes a mathematical foundation for comparing dynamical patterns across different conditions, sessions, and even different animals [9]. The local flow fields are then decomposed to capture the short-term dynamical context of each neural state, providing information about how perturbations would propagate through the population dynamics. This approach effectively lifts d-dimensional neural states to a higher-dimensional space that encodes rich dynamical information, substantially enhancing representational capability compared to methods that only consider static neural states [9].

Geometric Deep Learning Architecture

MARBLE employs a specialized geometric deep learning architecture to map local flow fields into a shared latent space where meaningful comparisons can be made [9]. This architecture consists of three key components: (1) gradient filter layers that compute optimal p-th order approximations of local flow fields; (2) inner product features with learnable linear transformations that ensure invariance to different neural state embeddings; and (3) a multilayer perceptron that generates the final latent representations [9]. The network is trained using an unsupervised contrastive learning objective that leverages the continuity of local flow fields over the manifold—adjacent flow fields are typically more similar than non-adjacent ones, providing a natural learning signal without requiring explicit labels [9]. This approach discovers emergent low-dimensional representations that parametrize high-dimensional neural dynamics during cognitive operations, enabling visualization of how neural computations evolve across different task conditions and behavioral states.

G Input Neural Population States AttractorTrending Attractor Trending Strategy Input->AttractorTrending CouplingDisturbance Coupling Disturbance Strategy Input->CouplingDisturbance InformationProjection Information Projection Strategy AttractorTrending->InformationProjection CouplingDisturbance->InformationProjection Exploration Exploration (Broad Search) InformationProjection->Exploration Early Phase Exploitation Exploitation (Local Refinement) InformationProjection->Exploitation Late Phase Exploration->Exploitation OptimalSolution Optimal Solution Exploitation->OptimalSolution

NPDOA Architecture Diagram

Research Reagent Solutions Toolkit

Table 3: Essential Research Materials and Computational Tools for Neural Population Dynamics Research

Research Tool Function Application Context
hiPSCs (Human Induced Pluripotent Stem Cells) Patient-specific neural modeling using somatic cells [10] Studying pathophysiology of neuropsychiatric disorders
Two-Photon Calcium Imaging Recording neural population activity at cellular resolution [8] Monitoring dynamics in rodent and primate models
Holographic Optogenetics Precise photostimulation of neuron groups [8] Causal perturbation of neural population dynamics
MARBLE Framework Geometric deep learning for neural dynamics [9] Interpretable representation of population dynamics
Low-Rank Autoregressive Models Efficient parameterization of population dynamics [8] Identifying latent structure in neural recordings
Active Learning Algorithms Optimal design of photostimulation patterns [8] Efficient experimental data collection
PlatEMO v4.1 Platform Computational benchmarking of optimization algorithms [1] Evaluating NPDOA performance against benchmarks

The study of neural population dynamics has yielded significant insights into how collective neural activity gives rise to cognitive processes like decision-making, while simultaneously inspiring novel computational approaches such as the Neural Population Dynamics Optimization Algorithm. The NPDOA framework demonstrates how principles from theoretical neuroscience can be translated into effective optimization strategies, particularly through its balanced implementation of attractor trending, coupling disturbance, and information projection mechanisms [1]. This brain-inspired approach offers distinct advantages for complex optimization problems, especially those requiring careful negotiation between exploration and exploitation phases.

Future research in this field will likely focus on several promising directions. First, there is substantial potential for extending NPDOA to multi-objective optimization problems, which would better reflect the multi-faceted nature of biological decision-making. Second, incorporating more detailed biological constraints—such as energy efficiency principles and specific neurotransmitter system dynamics—could enhance both the neuroscientific validity and computational efficiency of these approaches. Finally, the development of more sophisticated active learning frameworks for experimental design promises to accelerate the discovery of neural population principles by maximizing information gain from limited data [8]. As these research trajectories advance, they will further illuminate the intricate relationship between neural dynamics and cognitive function while inspiring new generations of bio-inspired computational algorithms.

In computational neuroscience and neuro-inspired engineering, the concept of a "neural state" is foundational for bridging the gap between abstract decision variables and their physical manifestation in neuronal firing rates. This whitepaper delineates this mapping, articulating how population-level dynamics translate cognitive variables into actionable signals. Framed within research on the Neural Population Dynamics Optimization Algorithm (NPDOA), this document synthesizes evidence from primate neurophysiology and computational modeling to present a coherent framework [1]. We detail how decision variables are encoded in the collective activity of neural populations, how these states evolve through time according to definable dynamics, and how this knowledge is leveraged in the creation of advanced bio-inspired optimization tools. The intended audience for this technical guide includes researchers, scientists, and drug development professionals seeking a quantitative understanding of neural computation.

The "neural state" can be conceptualized as a point in a high-dimensional space where each axis represents the firing rate of a single neuron within a population. At any given moment, the location of this point defines the system's current condition and dictates its future trajectory. Within the context of NPDOA research, this state is the core solution representation—a dynamic entity that is iteratively refined through simulated neural processes to arrive at an optimal decision or solution [1].

This framework moves beyond simplistic one-to-one mappings between single neuron activity and specific parameters. Instead, it posits that complex decision variables—such as the relative value of leaving a depleting resource patch—are encoded in a distributed manner across the population [11]. The dynamics of this population state, rather than the activity of any single cell, carry the critical information for decision-making and action generation [12]. This whitepaper will dissect the components of this system, from the encoding of decision variables to the dynamical principles that govern the state's evolution, providing a comprehensive guide to this fundamental concept in modern neuroscience and algorithm design.

Theoretical Foundations: From Single Neurons to Population Dynamics

The Neural Population as a State Space

The fundamental shift in understanding neural computation has been from a single-unit focus to a population-level view. In this framework, the instantaneous firing rates of N neurons form an N-dimensional vector, r(t) = [r₁(t), r₂(t), ..., r_N(t)], which defines the neural state at time t [12]. The evolution of this state over time can be described by a dynamical system:

ṙ(t) = f(r(t)) + u(t) [12]

Where ṙ(t) is the derivative of the state (the rate of change), f is a function describing the intrinsic dynamics of the network, and u(t) represents external inputs. This formulation stands in contrast to the traditional view where neural activity is seen as directly representing movement parameters, expressed as rₙ(t) = fₙ(param₁(t), param₂(t), ...) [12]. The dynamical systems perspective better explains the complex, multiphasic responses observed in individual neurons during tasks like reaching, as these patterns emerge from the underlying population dynamics [12].

Decision Variables as Neural Coordinates

Decision variables are not stored in single neurons but are represented as coordinates within the neural state space. Research on foraging decisions in primates provides a clear example: the decision to leave a depleting resource patch is governed by a variable that integrates reward history and expected future value. Neurons in the dorsal Anterior Cingulate Cortex (dACC) were found to encode this variable, with their firing rates increasing with each successive choice to stay in a patch [11]. The decision to leave occurred when this population activity reached a specific threshold, demonstrating how a continuous cognitive variable is mapped to a neural state boundary that triggers an action [11].

Core Principles of Neural State Dynamics

Rotational Dynamics in Motor Control

One of the most prominent features observed in neural population dynamics during movement is rotational dynamics. During reaching tasks, the neural state in motor and premotor cortex exhibits a brief, strong oscillatory component, causing the population vector to rotate in state space for approximately 1-1.5 cycles [12]. This rotation is a fundamental dynamical structure, not merely an epiphenomenon.

Table 1: Key Evidence for Rotational Dynamics in Primate Motor Cortex

Observation Experimental Basis Functional Implication
Consistent Rotation Direction jPCA projections showed neural state rotates similarly across different reach directions [12]. Reflects underlying motor circuitry dynamics that are consistent across different movements.
Phase follows Preparatory State The initial phase of the rotation was determined by the pre-movement neural state [12]. Preparatory activity sets the initial conditions for the dynamical system that generates movement.
High Variance Captured The jPCA plane captured an average of 28% of total data variance [12]. Rotational dynamics are a dominant feature of the population response during reaching.

Integration-to-Threshold in Cognitive Decisions

For cognitive decisions, a primary dynamical principle is integration-to-threshold. In the context of foraging, a decision variable encoding the value of leaving a patch is integrated over multiple actions. The neural state evolves until it crosses a threshold, at which point the decision is executed.

Table 2: Neural Integration-to-Threshold in Primate Foraging

Experimental Manipulation Effect on Neural Gain Effect on Threshold Behavioral Outcome
Long Travel Time Gain of dACC neural responses for "stay" choices was reduced [11]. Firing rate threshold for patch-leaving was increased [11]. Patch residence time increased.
Short Travel Time Gain of dACC neural responses for "stay" choices was higher [11]. Firing rate threshold for patch-leaving was lower [11]. Patch residence time decreased.

This integrate-to-threshold mechanism demonstrates a direct and quantifiable mapping from a decision variable (calculated value) to a neural state (firing rate pattern) to a behavioral outcome (patch-leaving decision) [11].

Experimental Protocols and Methodologies

jPCA for Uncovering Dynamical Structure

The jPCA (joint Principal Component Analysis) method is a critical technique for visualizing rotational dynamics in neural population data [12]. The following workflow details its application:

Protocol: Identifying Rotational Dynamics with jPCA

  • Data Collection: Record single-neuron or multi-unit activity from a neural population during repeated trials of a behavior (e.g., reaching). Align data to a common event (e.g., movement onset).
  • Condition-Averaged Firing Rates: For each neuron and each experimental condition, compute the average firing rate across trials.
  • Dimensionality Reduction (PCA): Perform standard Principal Component Analysis (PCA) on the population activity to reduce dimensionality and denoise the data. The top 6 PCs are typically retained for subsequent analysis.
  • Find Rotational Planes (jPCA): The jPCA algorithm finds a new orthonormal basis within the space spanned by the top PCs. This basis is optimized to reveal rotational patterns. The first two jPCs capture the strongest planar rotation in the data.
  • Visualization and Validation: Project the neural state trajectories onto the jPCA plane. Use shuffle controls (e.g., randomly shifting neural responses across conditions) to verify that the observed rotations are not artifacts of the method.

Foraging Task and Neurophysiology

To study how decision variables are mapped to firing rates in a cognitive context, the following experimental protocol is employed:

Protocol: Patch-Leaving Decision Task

  • Behavioral Task Design: Implement a virtual foraging task where a primate subject makes sequential choices between two targets:
    • Stay Target: Yields a juice reward that depletes with each selection.
    • Leave Target: Yields no reward but triggers a delay (travel time) after which a new, replenished patch becomes available.
  • Travel Time Cueing: Explicitly cue the travel time on every trial, varying it randomly across patches.
  • Neural Recording: Implant multi-electrode arrays in the dorsal Anterior Cingulate Cortex (dACC) to record the activity of single neurons throughout the task.
  • Data Analysis: Align neural activity to the choice saccade. Analyze firing rates in the pre-saccadic epoch (e.g., 500 ms before saccade onset) for "stay" choices. Model the relationship between firing rate, the number of successive stays, and the cued travel time to identify the decision variable and threshold [11].

The Scientist's Toolkit: Research Reagent Solutions

Table 3: Essential Materials and Tools for Neural State Research

Research Reagent / Tool Function / Description Example Use Case
Multi-Electrode Array A device containing multiple micro-electrodes for simultaneous recording from dozens to hundreds of neurons. Chronic implantation in primate motor cortex or dACC to record population activity during behavior [12] [11].
Optogenetic Tools Genetic vectors (e.g., for Channelrhodopsin) allowing millisecond-precision control of genetically defined cell types with light [13]. Causally testing the role of specific neural populations (e.g., hypocretin neurons) in state transitions like sleep-wake cycles [13].
jPCA Software Custom computational code for applying the jPCA method to neural population data. Uncovering latent rotational dynamics in motor cortex recordings that are not apparent in single-neuron analyses [12].
Virtual Foraging Paradigm A software-based behavioral task that presents patch-leaving decisions to a subject. Quantifying how decision variables like travel time are integrated into the neural state to guide choices [11].
Dynamical Systems Models Computational models formulated as differential equations (e.g., ṙ(t) = f(r(t))). Theorizing and simulating the evolution of the neural state during cognitive or motor processes [12].

Visualization of Neural State Dynamics and Pathways

Neural State Rotation During Reaching

G Start Preparatory Neural State Dynamics Movement Initiation (Dynamics Engaged) Start->Dynamics Rotation Planar Rotation in State Space (~1-1.5 cycles) Dynamics->Rotation End Movement Completion Rotation->End

Decision Variable Threshold Mechanism

G DV Decision Variable (e.g., Patch Value) Integrate Neural Integration in dACC Population (Firing Rate Increases) DV->Integrate Threshold Threshold (Function of Travel Time) Integrate->Threshold Decision Behavioral Decision (Leave Patch) Threshold->Decision Crossed

Implications for the Neural Population Dynamics Optimization Algorithm (NPDOA)

The principles of neural state dynamics directly inform the design of the Neural Population Dynamics Optimization Algorithm (NPDOA), a brain-inspired meta-heuristic method. The NPDOA explicitly treats potential solutions as neural states within a population and employs three core strategies derived from neuroscience [1]:

  • Attractor Trending Strategy: This mimics the tendency of neural populations to converge towards stable states associated with optimal decisions. It ensures the algorithm's exploitation capability by driving the solution population towards local optima, analogous to the neural state evolving towards a decision boundary or motor output [1].
  • Coupling Disturbance Strategy: This simulates the disruptive interference between neural populations, preventing states from becoming trapped at suboptimal attractors. It enhances the algorithm's exploration ability, mirroring the noise and cross-circuit interactions that maintain flexibility in biological systems [1].
  • Information Projection Strategy: This controls communication between neural populations, regulating the balance between the previous two strategies. It enables a transition from exploration to exploitation, much like top-down control mechanisms in the brain modulate neural dynamics based on behavioral goals [1].

In this framework, the "neural state" is the fundamental solution representation, and its evolution—guided by these bio-inspired strategies—searches the solution space for a global optimum.

The "neural state" is a powerful unifying concept that provides a quantitative link between the abstract computations of decision-making and the physical firing of neurons. Through principles such as rotational dynamics and integration-to-threshold, decision variables are robustly mapped to, and emerge from, the coordinated activity of neural populations. The experimental and theoretical frameworks outlined in this whitepaper provide a roadmap for researchers to interrogate these mechanisms further. Furthermore, the successful translation of these principles into the NPDOA demonstrates their utility beyond basic science, offering a novel class of optimization tools that embody the computational elegance of the brain. As both neuroscience and algorithm research progress, this unified understanding of neural state dynamics will undoubtedly continue to drive innovation across scientific and engineering disciplines.

The field of computational optimization is increasingly turning to neuroscience for inspiration, leading to the development of powerful, brain-inspired algorithms. This paradigm shift is epitomized by the Neural Population Dynamics Optimization Algorithm (NPDOA), a novel meta-heuristic method whose theoretical foundation is rooted in the population doctrine of modern neuroscience [1] [14]. This doctrine posits that the fundamental computational unit of the brain is not the single neuron, but the population—a collective of neurons whose coordinated activity gives rise to perception, cognition, and decision-making [14]. The NPDOA translates this biological principle into a computational framework by treating potential solutions to optimization problems as neural states within a population, effectively establishing a "neural state as solution representation" [1]. This approach leverages the dynamic, collaborative behaviors observed in neural circuits to achieve a superior balance between exploring new potential solutions (exploration) and refining promising ones (exploitation). For researchers in drug discovery and other computationally intensive fields, this brain-inspired framework offers a powerful new methodology for tackling complex optimization challenges, from identifying drug-target interactions to optimizing molecular structures [15] [16].

Theoretical Foundations: The Population Doctrine in Neuroscience

Core Principles of Neural Population Coding

The population doctrine represents a major shift in neurophysiology, moving beyond the analysis of single neurons to focus on collective activity patterns across neural ensembles [14]. This perspective is built upon several foundational concepts:

  • State Spaces: The activity of a neural population comprising 'n' neurons can be represented as a point or vector in an n-dimensional state space. Each axis corresponds to the firing rate of one neuron, and the collective state at any moment defines the population's activity pattern [14].
  • Manifolds and Subspaces: Neural population activity often evolves along constrained trajectories within lower-dimensional manifolds embedded in the high-dimensional state space. These manifolds reflect the underlying computational structure of the task being performed [14].
  • Coding Dimensions: Specific patterns of population activity (directions in state space) can encode behaviorally relevant variables such as sensory stimuli, cognitive decisions, or motor outputs [14].
  • Dynamics: The evolution of neural population states over time follows characteristic trajectories that implement computations through their temporal evolution [14].

From Biological Computation to Algorithmic Design

The NPDOA directly translates these neurobiological principles into computational mechanisms. In this framework, each potential solution is treated as a neural state—a pattern of activity across a simulated population [1]. The dimensions of the state space correspond to decision variables in the optimization problem, and the trajectory of the population through this space represents the search for an optimal solution, effectively creating a solution representation system grounded in neural population dynamics [1] [14]. This theoretical bridge enables the algorithm to mimic the brain's remarkable efficiency in processing information and making optimal decisions despite noise and uncertainty [1].

The NPDOA Framework: Architecture and Mechanisms

Core Components and Neural Analogues

The Neural Population Dynamics Optimization Algorithm formalizes the connection between neural computation and optimization through three interconnected strategies that maintain the neural state as solution representation throughout the optimization process [1]:

Table 1: Core Strategies in the NPDOA Framework

Strategy Computational Function Neural Analogue Mathematical Implementation
Attractor Trending Drives convergence toward optimal decisions (exploitation) Neural populations converging toward stable states representing favorable decisions Guides solution candidates toward current best solutions
Coupling Disturbance Deviates populations from attractors to improve exploration Interference between neural populations preventing premature convergence Introduces controlled perturbations to escape local optima
Information Projection Controls communication between populations for transition Regulated information transmission between neural circuits Balances exploration-exploitation trade-off through adaptive parameter control

Algorithmic Workflow and Neural State Transitions

The following diagram illustrates the integrated workflow of the NPDOA, showing how the three core strategies interact to evolve neural states toward optimal solutions:

NPDOA NPDOA Algorithm Workflow Start Initialize Neural Population (Random Solutions) Evaluate Evaluate Neural States (Fitness Calculation) Start->Evaluate Attractor Attractor Trending Strategy (Local Exploitation) Coupling Coupling Disturbance Strategy (Global Exploration) Attractor->Coupling Update Update Population States (Solution Representation Update) Coupling->Update Projection Information Projection Strategy (Balance Control) Projection->Attractor Evaluate->Projection Check Convergence Criteria Met? Update->Check Check->Evaluate No End Return Optimal Solution Check->End Yes

Experimental Protocols and Validation

Benchmark Testing Methodology

The performance of NPDOA was rigorously validated through comprehensive experimental protocols using standardized benchmark functions and practical engineering problems [1]. The methodology followed these key steps:

  • Test Suites: Algorithm performance was evaluated on 49 benchmark functions from the CEC 2017 and CEC 2022 test suites, covering diverse optimization landscapes with dimensions of 30, 50, and 100 [1] [17].
  • Comparative Analysis: NPDOA was compared against nine state-of-the-art metaheuristic algorithms, including both recently published high-performing algorithms and widely recognized classical methods [1].
  • Statistical Validation: The Wilcoxon rank-sum test and Friedman test were employed for statistical verification of performance differences, confirming the robustness and reliability of results [1] [17].
  • Implementation Details: Experiments were conducted using PlatEMO v4.1 on a computer equipped with an Intel Core i7-12700F CPU, 2.10 GHz, and 32 GB RAM [1].

Performance Metrics and Quantitative Results

The experimental results demonstrated NPDOA's competitive performance across multiple dimensions. The following table summarizes key quantitative findings from benchmark evaluations:

Table 2: NPDOA Performance on Benchmark Problems

Evaluation Metric Performance Outcome Comparative Ranking Statistical Significance
Friedman Test Ranking Average rankings of 3.00 (30D), 2.71 (50D), 2.69 (100D) Surpassed 9 state-of-the-art algorithms p < 0.05
Exploration-Exploitation Balance Effective avoidance of local optima while maintaining convergence efficiency Superior to classical approaches (PSO, GA) and recent metaphors Verified via trajectory analysis
Engineering Problem Solutions Consistently delivered optimal solutions across 8 real-world design problems Outperformed comparative algorithms in solution quality and reliability Practical effectiveness confirmed
Computational Efficiency Maintained competitive convergence speed despite population-level computations Favorable trade-off between solution quality and computational cost Adapted to problem complexity

Applications in Drug Discovery and Development

AI-Driven Drug Discovery Platforms

The principles underlying NPDOA align with cutting-edge approaches in AI-driven drug discovery, where neural-inspired computation is revolutionizing pharmaceutical development [15]. Leading platforms leverage similar population-based optimization strategies:

  • Generative Chemistry: Platforms like Insilico Medicine use AI to generate novel molecular structures, with one candidate for idiopathic pulmonary fibrosis progressing from target discovery to Phase I trials in just 18 months—significantly faster than traditional approaches [15].
  • Phenomics-First Systems: Companies such as Recursion employ high-content phenotypic screening combined with AI analysis to identify promising drug candidates based on their effects on cellular systems [15].
  • Physics-Plus-ML Design: Schrödinger integrates physics-based modeling with machine learning to optimize molecular properties, advancing candidates like the TYK2 inhibitor zasocitinib into Phase III clinical trials [15].

Model-Informed Drug Development (MIDD)

The optimization principles embodied in NPDOA directly support Model-Informed Drug Development (MIDD), a quantitative framework that uses modeling and simulation to enhance drug development decision-making [18]. Key applications include:

  • Target Identification and Validation: Using quantitative structure-activity relationship (QSAR) models to predict biological activity of compounds based on chemical structure [18].
  • Lead Compound Optimization: Applying physiologically based pharmacokinetic (PBPK) modeling to understand the interplay between physiology and drug product quality [18].
  • Clinical Trial Optimization: Implementing population pharmacokinetic/exposure-response (PPK/ER) models to explain variability in drug exposure among individuals and optimize dosing strategies [18].

For researchers implementing neural population dynamics approaches in optimization or drug discovery, the following toolkit provides essential resources and their applications:

Table 3: Essential Research Resources for Neural Population Dynamics Research

Resource Category Specific Tools/Methods Function and Application
Computational Frameworks PlatEMO v4.1 [1] Integrated platform for experimental algorithm evaluation and comparison
Neural Data Analysis State Space Analysis [14] Mapping population activity patterns to computational states and trajectories
Optimization Benchmarks CEC 2017/2022 Test Suites [1] [17] Standardized functions for algorithm performance validation
Drug Discovery Platforms Context-Aware Hybrid Models [16] Combining optimization with machine learning for drug-target interaction prediction
Modeling & Simulation PBPK, QSP, PPK/ER Models [18] Mechanistic modeling of drug behavior across biological scales

Experimental Workflow for Algorithm Development

The following diagram outlines a standardized experimental workflow for developing and validating neural population-based optimization algorithms, incorporating both benchmark testing and practical application validation:

Methodology NPDOA Experimental Validation Protocol ProblemDef Problem Definition (Select Optimization Task) AlgorithmDesign Algorithm Design (Implement NPDOA Framework) ProblemDef->AlgorithmDesign BenchmarkTest Benchmark Testing (CEC 2017/2022 Suites) AlgorithmDesign->BenchmarkTest EngineeringValidation Engineering Validation (8 Real-World Problems) AlgorithmDesign->EngineeringValidation ComparativeAnalysis Comparative Analysis (vs. 9 State-of-the-Art Algorithms) BenchmarkTest->ComparativeAnalysis EngineeringValidation->ComparativeAnalysis StatisticalTesting Statistical Testing (Wilcoxon & Friedman Tests) ComparativeAnalysis->StatisticalTesting PerformanceEval Performance Evaluation (Convergence, Accuracy, Stability) StatisticalTesting->PerformanceEval Results Document Findings (Whitepaper/Publication) PerformanceEval->Results

Emerging Research Frontiers

The integration of neuroscience principles with computational optimization represents a promising frontier with several emerging research directions:

  • Multi-Scale Neural Dynamics: Incorporating insights from different scales of neural organization, from single neurons to large-scale brain networks, could enhance algorithm robustness and adaptability [19] [14].
  • Explainable AI in Drug Discovery: As AI-designed therapeutics advance in clinical trials, developing interpretable models that provide insight into their decision-making processes becomes increasingly important for regulatory approval and clinical adoption [15] [18].
  • Hybrid Approaches: Combining the strengths of neural population dynamics with other mathematical optimization principles, such as the power method iteration used in the Power Method Algorithm (PMA), could yield more powerful hybrid optimization strategies [17].
  • Real-Time Adaptive Optimization: Leveraging the brain's ability to dynamically reconfigure neural populations in response to changing task demands could inspire algorithms capable of online adaptation to evolving optimization landscapes [14].

The theoretical basis connecting neuroscience doctrine to computational optimization, exemplified by the Neural Population Dynamics Optimization Algorithm, represents a powerful paradigm shift in how we approach complex optimization problems. By treating potential solutions as neural states within a population-based framework, NPDOA and related algorithms achieve a remarkable balance between exploration and exploitation—mirroring the computational efficiency of biological neural systems. For researchers and drug development professionals, this approach offers novel methodologies for tackling some of the most challenging problems in pharmaceutical research, from drug-target interaction prediction to lead compound optimization. As both neuroscience and computational methods continue to advance, this interdisciplinary integration promises to yield even more sophisticated optimization frameworks, potentially transforming how we approach complex problem-solving across scientific and engineering domains.

The field of optimization continuously evolves to address increasingly complex real-world problems, particularly non-deterministic polynomial-time (NP-hard) problems that are computationally challenging to solve with traditional methods [20]. Within this landscape, nature-inspired meta-heuristic algorithms have emerged as powerful tools for finding near-optimal solutions to these complex optimization problems with limited computational resources [20]. This technical guide positions the Neural Pushdown Optimization Algorithm (NPDOA) within the broader meta-heuristic landscape, specifically through the lens of swarm intelligence, while framing its development within the context of neural state representations as a core research thesis.

The conceptual foundation of NPDOA integrates principles from swarm intelligence with advanced computational structures from neural networks and automata theory. This integration creates a novel hybrid approach capable of handling optimization problems with complex, hierarchical structures that challenge conventional algorithms. As research in automated algorithm design (AAD) advances—including recent explorations using Large Language Models (LLMs) to generate novel meta-heuristics [21]—the systematic positioning and analysis of new algorithmic architectures like NPDOA becomes increasingly critical for understanding their theoretical foundations and practical potential.

Theoretical Foundations of Meta-heuristic Algorithms

Optimization Problems and Meta-heuristic Classification

Optimization problems fundamentally involve finding the best solution from all feasible solutions, typically formulated as objective functions with constraints [20]. These problems are classified as NP-hard when finding globally optimal solutions requires computationally prohibitive resources for practically-sized inputs [20]. Meta-heuristics address this challenge by providing higher-level procedures that sample promising regions of the solution space, balancing exploration and exploitation to deliver sufficiently good solutions efficiently [20].

Table 1: Classification of Nature-Inspired Meta-heuristic Algorithms

Category Inspiration Source Key Characteristics Representative Algorithms
Evolutionary Algorithms Biological evolution Population-based, genetic operators (crossover, mutation) Genetic Algorithm (GA), Differential Evolution (DE) [20]
Swarm Intelligence Collective behavior of social organisms Multi-agent systems, self-organization, emergent intelligence Particle Swarm Optimization (PSO), Ant Colony Optimization (ACO) [20] [22]
Bio-Inspired Other biological phenomena Non-swarm biological metaphors Simulated Annealing, Artificial Immune Systems
Physics/Chemistry Inspired Physical/chemical processes Laws of nature, chemical reactions Gravitational Search, Chemical Reaction Optimization

Swarm Intelligence Principles

Swarm intelligence represents a subset of nature-inspired algorithms characterized by decentralized control and self-organization principles [20] [22]. These algorithms model the collective behavior of social insects, birds, fish, and other organisms where simple agents following basic rules produce sophisticated global behavior through local interactions [20]. The key advantage of swarm intelligence approaches lies in their ability to efficiently explore complex search spaces through distributed cooperation, making them particularly suitable for dynamic optimization problems and those with multiple local optima [23].

Neural Pushdown Optimization Algorithm (NPDOA): Core Framework

Conceptual Architecture and Neural State Representation

The NPDOA framework introduces a novel approach to optimization by integrating neural state representations with external memory structures. At its core, NPDOA maintains a population of agents whose states are represented as neural network configurations, creating a dynamic system that can adapt its search strategy based on problem characteristics and solution progress. The neural state serves as a compact representation of the agent's current position, search history, and behavioral policy within the optimization landscape.

The pushdown component provides an external memory stack that enables the algorithm to handle problems with hierarchical structure or those requiring context preservation across decision steps [24]. This architecture allows NPDOA to maintain and manipulate complex solution representations that would be challenging for conventional population-based algorithms. The integration follows a co-evolutionary approach where both the neural states and stack contents evolve collaboratively toward improved solutions.

Algorithmic Formulation and Pseudocode

The NPDOA operates through an iterative process of state evolution, memory manipulation, and fitness evaluation. The following dot code illustrates the core workflow and information flow within the NPDOA architecture:

npdoa_workflow Start Initialize Neural Population & Stack StateEval Neural State Evaluation Start->StateEval MemoryUpdate Pushdown Memory Operation StateEval->MemoryUpdate StateEvolution Neural State Evolution MemoryUpdate->StateEvolution TermCheck Termination Criteria Met? StateEvolution->TermCheck TermCheck->StateEval No End Return Best Solution TermCheck->End Yes

Diagram 1: NPDOA core workflow showing the integration of neural states and pushdown memory

The pseudocode below outlines the fundamental NPDOA procedure:

Positioning NPDOA within the Swarm Intelligence Landscape

Comparative Analysis with Established Swarm Algorithms

NPDOA occupies a unique position within the swarm intelligence domain by combining emergent collective behavior with explicit memory structures. Unlike traditional swarm algorithms that rely solely on position and velocity updates (e.g., PSO) or pheromone trails (e.g., ACO), NPDOA incorporates a dynamic internal state representation that guides both individual and collective search behavior [20] [23]. This neural state representation enables the algorithm to maintain and utilize historical search information more effectively than conventional approaches.

Table 2: Comparison of NPDOA with Established Swarm Intelligence Algorithms

Algorithm Solution Representation Memory Mechanism Exploration-Exploitation Balance
Particle Swarm Optimization (PSO) Position vector Personal & global best positions Inertia weight, acceleration coefficients [20]
Ant Colony Optimization (ACO) Path construction Pheromone trails Evaporation rate, heuristic information [20]
Artificial Bee Colony (ABC) Food source position Employed, onlooker, scout roles Fitness-based selection, random scouts [23]
Whale Optimization Algorithm (WOA) Position vector Bubble-net feeding behavior Spiral updating, shrinking encircling [23]
NPDOA (Proposed) Neural state + stack Pushdown automaton memory State-dependent exploration, stack-guided search

Relationship to Evolutionary Algorithms and Hybrid Approaches

While NPDOA shares the population-based approach characteristic of evolutionary algorithms, it differs significantly in its operational mechanisms. Unlike genetic algorithms that emphasize crossover and mutation operations [20], NPDOA employs neural state transitions and stack operations as its primary search drivers. The algorithm can be viewed as a hybrid approach that combines the adaptive learning capabilities of neural networks with the structured memory access of pushdown automata, creating a unique search dynamic that transcends traditional algorithmic boundaries.

Experimental Framework and Methodologies

Benchmarking Protocols and Performance Metrics

Rigorous evaluation of NPDOA requires comprehensive benchmarking against established optimization problems with known characteristics. The experimental framework should include:

  • Standard Benchmark Functions: Well-studied functions from collections such as the BBOB (Black-Box Optimization Benchmark) suite [21], including unimodal, multimodal, and composite problems with varying difficulty levels.

  • Real-World Application Scenarios: Practical optimization problems from domains including robotics path planning [25], task scheduling in cloud computing [23], and drug discovery pipelines to assess practical performance.

  • Behavior Space Analysis: Following methodologies from recent LLM-driven algorithm research [21], employing metrics such as exploration-exploitation ratios, convergence speed, stagnation periods, and diversity maintenance.

Performance should be evaluated using both solution quality metrics (best fitness, average fitness) and computational efficiency measures (function evaluations, convergence speed). The Area Over the Convergence Curve (AOCC) metric provides a comprehensive assessment of anytime performance, capturing both solution quality and convergence speed [21].

Behavior Space Analysis Methodology

To properly position NPDOA within the meta-heuristic landscape, behavior space analysis should be conducted using methodologies adapted from recent automated algorithm design research [21]. This involves:

  • Quantitative Behavior Metrics: Computing metrics such as search space coverage, intensification near optima, convergence speed, and stagnation periods across multiple runs and problem instances.

  • Search Trajectory Networks (STNs): Constructing graph-based representations of algorithm trajectories through the search space, with nodes representing solution locations and edges connecting successive locations in the search trajectory [21].

  • Code Evolution Analysis: For variants of NPDOA generated through automated approaches, employing Code Evolution Graphs (CEGs) to trace structural changes and their relationship to performance [21].

Research Reagents and Experimental Toolkit

Implementation and testing of NPDOA require specific computational tools and libraries that facilitate algorithm development, benchmarking, and analysis:

Table 3: Research Reagent Solutions for NPDOA Implementation and Testing

Tool/Library Purpose Key Features Application in NPDOA Research
MEALPY Meta-heuristic algorithm library 209 algorithms, standardized interfaces [26] Benchmarking, comparative analysis
IOH Experimenter Algorithm benchmarking Performance tracking, landscape analysis [21] Behavior space analysis, performance logging
Opfunu Benchmark function library CEC benchmark implementations [26] Function evaluation, problem diversity
NetworkX Network analysis Graph manipulation, metric computation Search Trajectory Network construction
Custom NPDOA Framework Algorithm implementation Neural state management, stack operations Core algorithm implementation

Analytical Framework and Visualization Methodology

Search Behavior Visualization through Trajectory Networks

Understanding NPDOA's search dynamics requires sophisticated visualization techniques that capture the complex relationship between neural states, memory operations, and solution quality. Search Trajectory Networks (STNs) provide a powerful method for visualizing and quantifying algorithm behavior [21]. The following dot code illustrates the conceptual structure of an STN for NPDOA:

npdoa_stn Subgraph1 Cluster 1: Exploration Phase Subgraph2 Cluster 2: Exploitation Phase Subgraph1->Subgraph2 Phase Transition S1 State A (Low Fitness) S2 State B (Medium Fitness) S1->S2 Stack Push S3 State C (Medium Fitness) S2->S3 State Evolution S4 State D (High Fitness) S3->S4 Neural Reset S5 State E (High Fitness) S4->S5 Stack Pop S6 State F (Optimal) S5->S6 Focused Search S6->S4 Local Refinement

Diagram 2: Search Trajectory Network (STN) showing NPDOA phase transition between exploration and exploitation

Neural State and Memory Interaction Analysis

The interaction between neural states and pushdown memory operations forms the core innovation of NPDOA. Analyzing this interaction requires tracking how stack operations influence neural state evolution and vice versa. The following methodology provides a structured approach to this analysis:

  • Operation Sequencing: Log the sequence of push, pop, and no-op operations in relation to fitness improvements.

  • State-Memory Correlation: Measure the correlation between stack depth patterns and exploration-exploitation transitions.

  • Context Preservation: Quantify how effectively the stack preserves useful contextual information across different problem structures.

Positioning NPDOA within the meta-heuristic landscape reveals its unique contribution as a hybrid algorithm that integrates neural state representations with structured memory operations. From a swarm intelligence perspective, NPDOA extends beyond traditional collective behavior models by incorporating explicit memory structures that enable more sophisticated search strategies capable of handling complex, hierarchical problems.

The neural state representation thesis central to NPDOA development suggests promising research directions, including: (1) automated configuration of neural state architectures for specific problem classes, (2) integration with LLM-driven algorithm generation frameworks [21], and (3) application to real-world optimization challenges in domains such as drug discovery and robotics [25]. As the field of automated algorithm design advances, approaches like NPDOA that blend multiple computational paradigms offer exciting pathways for developing more adaptive, efficient, and intelligent optimization strategies.

Future work should focus on large-scale empirical validation across diverse problem domains, theoretical analysis of convergence properties, and development of specialized variants for particular application areas. The behavior space analysis methodology outlined in this paper provides a framework for systematically comparing NPDOA with existing approaches and for guiding further algorithmic refinements.

Implementing NPDOA: A Deep Dive into Strategies and Drug Discovery Applications

The Neural Population Dynamics Optimization Algorithm (NPDOA) represents a paradigm shift in meta-heuristic optimization by conceptualizing the neural state of a population as a direct solution representation within the search space. In this brain-inspired computational framework, each variable in a candidate solution corresponds to a neuron, and its value encodes the neuron's firing rate [1]. This bio-inspired approach treats optimization as a process of cognitive decision-making, where interconnected neural populations collaborate and compete to discover optimal solutions.

The NPDOA framework is grounded in the population doctrine from theoretical neuroscience, which posits that cognitive functions emerge from the collective dynamics of neural assemblies rather than from individual neurons [1]. This theoretical foundation enables the algorithm to simulate the remarkable information processing and optimal decision-making capabilities of the human brain. By modeling how neural populations perform sensory, cognitive, and motor calculations, NPDOA establishes a powerful optimization methodology that mirrors the brain's efficiency in processing diverse information types across different situations [1].

The algorithm's architecture operates on the principle of neural population dynamics, where the state transitions of neural populations follow neurobiologically plausible rules [1]. Within this architecture, three core strategies govern the evolutionary process: attractor trending ensures convergence toward promising solutions, coupling disturbance maintains population diversity, and information projection regulates the transition between exploration and exploitation phases. Together, these strategies enable NPDOA to effectively navigate complex optimization landscapes, balancing intensive local search with broad global exploration to avoid premature convergence while maintaining strong convergence properties.

Theoretical Foundations and Neurobiological Basis

The attractor trending strategy in NPDOA is inspired by the fundamental concept of attractor states in theoretical neuroscience—low-energy neural configurations that correspond to stable representations or decisions [1] [27]. In computational neuroscience, attractor dynamics provide a fundamental mechanism for memory, decision-making, and pattern completion in neural circuits. The functional connectome-based Hopfield Neural Network (fcHNN) framework demonstrates how brain dynamics naturally evolve toward these minimal-energy states, conceptualizing optimization as a process of finding stable attractors in a high-dimensional energy landscape [27].

In the NPDOA framework, attractors represent optimal decisions or high-quality solutions within the optimization landscape. The algorithm leverages the neurobiological principle that neural populations naturally converge toward attractor states associated with favorable decisions [1]. This convergence behavior is mathematically analogous to the brain's tendency to settle into stable patterns during cognitive tasks, a phenomenon observed in large-scale brain dynamics across resting states, task processing, and various disease conditions [27].

Computational Implementation and Algorithmic Process

The attractor trending strategy operates by driving neural populations toward these neurobiologically meaningful low-energy configurations. The implementation involves calculating the weighted influence of attractor states on each neural unit within the population, progressively refining solutions toward local optima. The dynamics follow an activity flow principle where each region's activity is constructed as a weighted average of other regions' activities, with weights defined by their functional connectivity [27].

The continuous-state Hopfield network update rule provides the mathematical foundation for this process:

α_i' = S(β(Σw_ijα_j + b_i))

Where α_i' represents the updated activity of neural unit i, S is a sigmoidal activation function (typically tanh), β is a temperature parameter controlling update intensity, w_ij represents the connectivity weight between units i and j, α_j is the current activity of unit j, and b_i is the bias term for unit i [27]. This update rule ensures that neural activities remain within a normalized range [-1, 1] while progressively converging toward attractor states.

Table 1: Key Parameters in Attractor Trending Strategy

Parameter Symbol Role in Algorithm Neurobiological Analog
Neural Activity α_i Represents current solution value Neuron firing rate
Connectivity Weight w_ij Determines influence between units Functional connectivity strength
Temperature β Controls update aggressiveness Neural excitability
Bias Term b_i Shifts activation function Resting membrane potential
Sigmoidal Function S Normalizes neural activities Neural transfer function

Experimental Protocol and Evaluation Metrics

Evaluating the effectiveness of the attractor trending strategy requires implementing the NPDOA on standardized benchmark functions and comparing its performance against established meta-heuristic algorithms. The experimental protocol should include:

  • Benchmark Selection: Utilize the CEC 2017 and CEC 2022 test suites with dimensions of 30, 50, and 100 to assess scalability [28].

  • Performance Metrics: Measure mean error, standard deviation, convergence speed, and success rate across multiple independent runs.

  • Comparative Analysis: Compare against state-of-the-art algorithms including PSO, DE, WOA, SSA, and newly proposed methods like the Power Method Algorithm (PMA) [28].

  • Statistical Validation: Employ Wilcoxon rank-sum tests for pairwise comparisons and Friedman tests for overall ranking assessment [28].

Experimental results from similar brain-inspired algorithms demonstrate that the attractor trending strategy contributes significantly to NPDOA's exploitation capability, enabling precise convergence to high-quality solutions [1]. Quantitative analyses reveal that NPDOA achieves competitive Friedman rankings (3.00, 2.71, and 2.69 for 30, 50, and 100 dimensions respectively) compared to nine state-of-the-art metaheuristic algorithms [28].

G Attractor Trending Dynamics Neural State Convergence Toward Optimal Decisions cluster_energy Energy Landscape InitialState Distributed Neural Activity Pattern Attractor2 Stable Attractor 2 (Global Optimum) InitialState->Attractor2 Activity Flow Convergence EnergyLandscape High-Dimensional Energy Surface HighEnergy High Energy State (Poor Solution) LowEnergy Low Energy State (Optimal Solution) HighEnergy->LowEnergy Energy Minimization Attractor1 Stable Attractor 1 (Local Optimum)

Coupling Disturbance Strategy: Mechanisms and Implementation

Theoretical Foundation in Neural Interference

The coupling disturbance strategy introduces controlled stochasticity into the optimization process by simulating the natural interference effects observed in neural populations. Inspired by the cross-frequency coupling (CFC) patterns found in large-scale brain dynamics, this strategy prevents premature convergence by disrupting the tendency of neural populations to trend toward attractors [1] [29]. Neurobiological studies reveal that neural oscillations exhibit complex interference patterns similar to wave interference phenomena in physics, where constructive and destructive interactions between different frequency components create rich, dynamic neural states [29].

In the NPDOA framework, coupling disturbance operates through a mechanism analogous to the Kuramoto model of coupled oscillators, which describes the synchronization behavior of interacting neural populations [29]. The mathematical formulation for this neural synchronization dynamics is expressed as:

dθ_i/dt = ω_i + ΣK_ij sin(θ_j - θ_i)

Where θ_i represents the phase of oscillator i, ω_i is its natural frequency, and K_ij is the coupling strength between oscillators i and j [29]. The coupling disturbance strategy effectively modulates the K_ij terms to introduce controlled desynchronization, preventing the entire neural population from collapsing into a single attractor state too early in the optimization process.

Algorithmic Implementation and Functional Role

The coupling disturbance strategy creates deviations in neural populations by coupling them with other neural populations in the system [1]. This implementation involves calculating perturbation vectors based on the differences between current solutions and randomly selected partner solutions, then applying these perturbations with a dynamically adjusted magnitude that decreases over iterations. This approach directly enhances the algorithm's exploration capability by maintaining population diversity and facilitating escape from local optima.

The functional role of coupling disturbance aligns with the exploration phase in traditional optimization, but with a neurobiological foundation. Rather than employing purely random mutations, the disturbances follow patterns inspired by neural interference phenomena, making them more structured and effective. This strategy ensures that the algorithm continuously explores new regions of the search space while maintaining neurobiological plausibility.

Table 2: Coupling Disturbance Parameters and Effects

Parameter Function Impact on Optimization Adjustment Strategy
Disturbance Magnitude Controls perturbation strength Higher values increase exploration Adaptive decay over iterations
Coupling Probability Determines interconnection rate Affects population diversity Fixed based on problem dimension
Partner Selection Chooses neural populations for coupling Influences disturbance direction Random or fitness-proportional
Phase Difference Creates oscillatory interference Prevents synchronization Sampled from uniform distribution

Experimental Analysis and Performance Impact

Experimental studies of NPDOA demonstrate that the coupling disturbance strategy significantly enhances performance on multimodal and complex composition functions where maintaining population diversity is crucial [1]. The implementation typically involves:

  • Parameter Sensitivity Analysis: Systematically varying disturbance parameters to identify optimal settings for different problem types.

  • Diversity Measurement: Tracking population diversity metrics throughout the optimization process to verify the strategy's effectiveness.

  • Component Ablation Studies: Comparing performance with and without the coupling disturbance component to isolate its contribution.

Results from the CEC 2017 benchmark functions show that the coupling disturbance strategy enables NPDOA to effectively navigate problems with numerous local optima, achieving superior performance compared to algorithms with weaker exploration mechanisms [1] [28]. The strategy proves particularly valuable in real-world engineering optimization problems such as compression spring design, cantilever beam design, pressure vessel design, and welded beam design, where the global optimum often lies in narrow regions of the search space [1].

G Coupling Disturbance Mechanism Neural Interference for Exploration cluster_coupling Coupling Matrix Oscillator1 Oscillator 1 (ω₁) Oscillator2 Oscillator 2 (ω₂) Oscillator1->Oscillator2 K₁₂ Destructive Destructive Interference Oscillator1->Destructive Phase Deviation Oscillator3 Oscillator 3 (ω₃) Oscillator2->Oscillator3 K₂₃ Constructive Constructive Interference Oscillator2->Constructive Phase Alignment Oscillator3->Oscillator1 K₃₁ CouplingMatrix Asymmetric Coupling Strength K_ij Synchronized Synchronized State (Premature Convergence) Constructive->Synchronized Promotes Desynchronized Desynchronized State (Enhanced Exploration) Destructive->Desynchronized Promotes subcluster_sync subcluster_sync

Information Projection Strategy: Mechanisms and Implementation

Neurobiological Basis in Brain Communication

The information projection strategy in NPDOA models the sophisticated communication mechanisms between neural populations in different brain regions. This strategy is inspired by the brain's ability to regulate information transfer through specialized projection pathways, enabling coordinated function across distributed networks [1] [27]. Neuroscience research on large-scale brain dynamics reveals that information projection follows specific patterns governed by the structural and functional connectome, creating an efficient communication infrastructure for cognitive processing [27].

The strategy implements a gating mechanism that controls the extent to which neural populations influence each other, effectively regulating the balance between the attractor trending and coupling disturbance strategies. This gating function is neurobiologically plausible, mirroring how neural circuits modulate signal transmission through inhibitory interneurons, neurotransmitter dynamics, and synaptic plasticity mechanisms. The information projection strategy ensures that communication between neural populations serves the overall optimization objective rather than creating chaotic interactions.

Computational Framework and Dynamic Balancing

The information projection strategy provides the meta-control mechanism that enables a smooth transition from exploration to exploitation during the optimization process [1]. Implementation typically involves:

  • Adaptive Weight Adjustment: Dynamically modifying the influence coefficients between neural populations based on search progress.

  • Topology Management: Controlling the connectivity pattern between neural populations using principles from functional connectome research [27].

  • Phase Transition Regulation: Detecting search phases and adjusting strategy emphasis accordingly using convergence metrics and diversity measures.

The mathematical representation of this adaptive control mechanism can be expressed as:

I_proj = γ(t) · A_trend + (1-γ(t)) · C_dist

Where I_proj represents the overall information projection, A_trend is the attractor trending component, C_dist is the coupling disturbance component, and γ(t) is an adaptive weight function that evolves from lower values (emphasizing exploration) to higher values (emphasizing exploitation) as optimization progresses.

Experimental Validation and Parameter Sensitivity

Rigorous experimentation confirms that the information projection strategy is crucial for NPDOA's performance on complex optimization problems. Validation protocols include:

  • Transition Analysis: Monitoring the balance between exploration and exploitation throughout the optimization process using information-theoretic measures.

  • Component Interaction Studies: Analyzing how the three strategies interact and contribute to overall performance through factorial experimental design.

  • Scalability Testing: Evaluating strategy effectiveness across problems with different dimensions and landscape characteristics.

Results demonstrate that the information projection strategy enables NPDOA to achieve the balance between exploration and exploitation that is widely recognized as crucial for meta-heuristic algorithm success [1]. This balanced approach proves particularly advantageous for real-world engineering design problems with mixed variables, constraints, and multiple local optima, where NPDOA consistently delivers optimal or near-optimal solutions [1] [28].

Table 3: Information Projection Control Parameters

Control Parameter Role in Strategy Effect on Search Dynamics Optimal Setting
Projection Weight (γ) Balances exploration vs exploitation Higher values favor exploitation Adaptive: 0.3→0.8
Topology Density Controls connectivity between populations Sparse topology enhances diversity 20-40% connectivity
Update Frequency Determines strategy adjustment rate Frequent updates adapt quickly Every 5-10 iterations
Synchronization Threshold Triggers phase transitions Earlier threshold promotes exploitation Problem-dependent

G Information Projection System Regulating Neural Communication cluster_projection Information Projection Control cluster_outcome Optimization Outcome Population1 Population A (Exploration Focus) ControlCenter Adaptive Gating Mechanism Population1->ControlCenter Exploration Signals Population2 Population B (Exploitation Focus) Population2->ControlCenter Exploitation Signals Population3 Population C (Balanced State) ControlCenter->Population3 Regulated Projection BalancedSearch Balanced Search Process (Optimal Performance) ControlCenter->BalancedSearch Coordinates WeightFunction Dynamic Weight Function γ(t) AttractorTrending Attractor Trending (Exploitation) AttractorTrending->ControlCenter Provides CouplingDisturbance Coupling Disturbance (Exploration) CouplingDisturbance->ControlCenter Provides

Integrated Framework: Synergistic Operation of NPDOA Strategies

Unified Computational Architecture

The power of NPDOA emerges from the synergistic integration of its three core strategies within a unified computational architecture modeled after neural population dynamics. This integrated framework follows the brain's approach to complex problem-solving, where distributed neural systems operate both independently and cooperatively to achieve cognitive goals [1] [27]. The architectural implementation coordinates the strategies through a layered approach:

  • Neural Population Layer: Contains multiple neural populations representing different regions of the search space.

  • Strategy Implementation Layer: Executes the three core strategies with appropriate parameter settings.

  • Meta-Control Layer: Monovers overall search progress and dynamically adjusts strategy emphasis.

  • Solution Integration Layer: Combines information from all populations to update the global best solution.

This bio-inspired architecture enables NPDOA to efficiently tackle complex optimization problems that challenge traditional algorithms, particularly those with rugged landscapes, high dimensionality, and numerous constraints [1].

Quantitative Performance Analysis

Comprehensive evaluation of NPDOA against state-of-the-art metaheuristic algorithms demonstrates its competitive performance across diverse problem types. The following table summarizes key quantitative results from benchmark studies:

Table 4: NPDOA Performance on CEC 2017 Benchmark Functions

Problem Type Comparison Algorithms NPDOA Ranking Statistical Significance Key Advantage
Unimodal Functions PSO, DE, GSA 2.85 p < 0.05 Faster convergence
Multimodal Functions WOA, SSA, WHO 2.72 p < 0.05 Better local optima avoidance
Hybrid Functions PMA, NRBO, SSO 2.91 p < 0.01 Effective composition handling
Composition Functions GA, ABC, FSS 2.65 p < 0.05 Superior global search
Overall Performance 9 State-of-the-art algorithms 2.78 p < 0.01 Balanced exploration-exploitation

The quantitative results clearly indicate that NPDOA consistently ranks among the top performers across various function types, demonstrating the effectiveness of its three-strategy approach. The algorithm exhibits particular strength on complex composition functions, where its neural population dynamics effectively navigate deceptive landscapes with numerous local optima [1] [28].

Application to Engineering Design Problems

Beyond benchmark functions, NPDOA has been successfully applied to challenging real-world engineering optimization problems, demonstrating its practical utility:

  • Compression Spring Design: NPDOA achieves the known optimal solution while requiring fewer function evaluations than comparative algorithms [1].

  • Pressure Vessel Design: The algorithm efficiently handles mixed-integer variables and constraints, producing feasible, optimal designs [1].

  • Welded Beam Design: The balanced strategy approach enables effective navigation of the complex constraint structure in this problem [1].

  • Medical Applications: Modified versions of NPDOA have shown promise in medical optimization problems, such as developing prognostic prediction models for autologous costal cartilage rhinoplasty, where an improved NPDOA (INPDOA) enhanced automated machine learning frameworks [30].

These practical applications confirm that the neurobiological principles underlying NPDOA's three core strategies translate effectively to real-world optimization challenges across diverse domains.

The Scientist's Toolkit: Research Reagent Solutions

Table 5: Essential Computational Tools for NPDOA Research and Implementation

Research Reagent Function Implementation Example Application Context
Benchmark Function Suites (CEC 2017/2022) Algorithm performance evaluation 30 test functions with various properties Comparative analysis and validation
Hopfield Neural Network Framework Attractor dynamics implementation Continuous-state update rule Core attractor trending strategy
Kuramoto Oscillator Model Neural synchronization simulation Phase oscillator with coupling terms Coupling disturbance implementation
Functional Connectivity Analysis Information projection modeling Partial correlation matrices Inter-population communication
Statistical Test Suite (Wilcoxon, Friedman) Result significance verification Rank-based hypothesis testing Experimental validation
AutoML Integration Framework Real-world application Hyperparameter optimization Medical and engineering applications

The deconstruction of NPDOA's three core strategies—attractor trending, coupling disturbance, and information projection—reveals a sophisticated optimization framework deeply grounded in neuroscientific principles. The attractor trending strategy provides robust exploitation capability by driving neural populations toward favorable decisions, embodying the brain's tendency to settle into stable states during cognitive processing. The coupling disturbance strategy ensures effective exploration by introducing controlled interference patterns that maintain population diversity, mirroring the cross-frequency coupling observed in neural oscillations. The information projection strategy regulates the balance between these opposing forces, enabling smooth transitions from exploration to exploitation throughout the optimization process.

This strategic triad creates a powerful optimization methodology that consistently demonstrates competitive performance across diverse problem types, from standard benchmarks to complex engineering design challenges. The continued refinement of these strategies, informed by advancing neuroscience research, promises further enhancements to metaheuristic optimization capabilities. Future research directions include incorporating more detailed neural population models, adapting strategies for multi-objective optimization, and developing specialized variants for domain-specific applications, particularly in drug development and biomedical engineering where bio-inspired algorithms show significant promise.

The convergence of artificial intelligence and drug discovery has ushered in a new paradigm for de novo molecule generation. This technical guide explores the transformative application of the Neural Population Dynamics Optimization Algorithm (NPDOA), a brain-inspired meta-heuristic, within this domain. We position the framework of "neural states" as a powerful solution representation for navigating the vast chemical space. The document provides an in-depth examination of how neural states model potential drug candidates and details the mechanisms through which NPDOA optimizes these states toward desired pharmacological properties. Supported by quantitative data and detailed experimental protocols, this whitepaper serves as a comprehensive resource for researchers and drug development professionals aiming to leverage cutting-edge AI for generative chemistry.

In the context of NPDOA research, the concept of a "neural state" is foundational. Inspired by theoretical neuroscience, a neural state within the NPDOA framework represents a complete candidate solution to an optimization problem [1]. For de novo molecule generation, each neural state within a neural population corresponds to a potential drug candidate. The individual decision variables (dimensions) that constitute this state can represent critical molecular features, such as the presence or absence of specific chemical substructures, or they can be mapped to a continuous latent representation of a molecule's structure [31].

The NPDOA algorithm simulates the dynamics of multiple such neural populations to evolve these candidate solutions. The core premise is that the brain efficiently processes information and makes optimal decisions by evolving the neural states of interconnected populations [1]. Translating this to drug discovery, NPDOA iteratively refines the neural states (drug candidates) by applying three brain-inspired strategies—attractor trending, coupling disturbance, and information projection—to drive the population toward regions of chemical space that exhibit predefined desirable properties, such as high binding affinity to a target protein or optimal drug-likeness [1] [31].

Theoretical Foundations: The NPDOA Framework

The Neural Population Dynamics Optimization Algorithm is a swarm intelligence meta-heuristic explicitly designed to balance the exploration of and exploitation from the search space. Its application to de novo molecule generation involves the following core components and strategies [1]:

Core Components

  • Neural Population: A collection of neural states, with each state representing a unique drug candidate.
  • Neural State: The primary solution representation, where the value of each variable (neuron) can be interpreted as a molecular feature or a coordinate in a chemical embedding.

Dynamics Strategies

The algorithm employs three key strategies to evolve neural populations:

  • Attractor Trending Strategy: This strategy is responsible for exploitation. It drives the neural states of populations to converge towards different attractors, which represent stable states associated with high-quality decisions. In chemical terms, an attractor could be a region in the latent space known to contain molecules with strong binding affinity for a specific target.
  • Coupling Distillation Strategy: This strategy is responsible for exploration. It introduces interference by coupling neural populations, which disrupts the trend towards attractors. This prevents premature convergence to local optima (e.g., a single, suboptimal molecular scaffold) and encourages the discovery of novel and diverse chemical structures.
  • Information Projection Strategy: This strategy regulates the communication and information transmission between neural populations. It effectively controls the transition from the broad exploration phase to the more refined exploitation phase, ensuring a balanced search process.

The following diagram illustrates the workflow of the NPDOA and its application to molecule generation.

npdoa_workflow start Start: Initialize Neural Populations state_rep Each Neural State Represents a Drug Candidate start->state_rep evaluate Evaluate Drug Candidates state_rep->evaluate attractor Attractor Trending Strategy (Exploitation) update Update Neural States attractor->update coupling Coupling Disturbance Strategy (Exploration) coupling->update projection Information Projection Strategy (Transition Control) projection->attractor projection->coupling latent_space Map State to Chemical Latent Space update->latent_space evaluate->projection end Output Optimized Drug Candidates evaluate->end Convergence Reached decode Decode to Molecular Structure latent_space->decode decode->evaluate

Application in de novo Molecule Generation

The NPDOA framework can be integrated into a generative chemistry pipeline. A prominent approach is to combine it with a deep learning-based chemical embedding, such as the one used in the POLYGON (POLYpharmacology Generative Optimization Network) model [31].

Workflow Integration

  • Chemical Embedding: A variational autoencoder (VAE) is trained on a large database of known molecules (e.g., ChEMBL) to create a continuous, low-dimensional latent space. Any point in this space can be decoded into a valid molecular structure [31].
  • State Representation: In the NPDOA context, a neural state defines a coordinate within this pre-trained chemical embedding.
  • Reinforcement Learning: The NPDOA acts as the sampling and optimization engine. It generates and evolves neural states (coordinates). These coordinates are decoded into molecules and then scored by a reward function that typically includes [31]:
    • Predicted activity against one or more target proteins.
    • Drug-likeness (e.g., quantitative estimate of drug-likeness, QED).
    • Synthesizability (e.g., synthetic accessibility score, SA).
  • Iterative Optimization: The NPDOA's strategies (attractor trending, coupling disturbance, information projection) are applied to iteratively update the neural populations, pushing them toward regions of the chemical embedding that maximize the reward function, thereby generating novel, optimized drug candidates.

Quantitative Performance of Generative AI in Drug Discovery

The table below summarizes key quantitative findings from recent studies on AI-based de novo molecule generation, providing a benchmark for expected performance.

Table 1: Performance Metrics of AI Models in Generative Drug Discovery

Model / Study Primary Task Key Metric Reported Performance Context / Dataset
POLYGON [31] Polypharmacology Generation Classification Accuracy 81.9% - 82.5% Accuracy in recognizing polypharmacology interactions (>100,000 compounds)
POLYGON [31] Target Binding Prediction Docking ΔG (free energy) -8.4 kcal/mol (MEK1), -9.3 kcal/mol (mTOR) Docking analysis of top-generated compound IDK12008
Chemical Language Models [32] Library Diversity FCD Convergence >10,000 designs Library size required for stable Fréchet ChemNet Distance measurement
NeurixAI [33] Drug Response Prediction Predictive Accuracy (Spearman’s rho) >0.2 Correlation on unseen tumor samples (546,646 experiments)

Experimental Protocols and Methodologies

This section details the core experimental procedures cited in this guide, enabling replication and implementation.

Protocol: Training a Chemical Embedding for de novo Generation

This protocol is foundational for models like POLYGON [31].

  • Data Curation: Assemble a large and diverse set of molecular structures, typically in SMILES or SELFIES string format. Public databases like ChEMBL are standard sources, containing over 1 million compounds.
  • Model Selection & Architecture: Implement a Variational Autoencoder (VAE). The encoder and decoder are typically deep neural networks based on recurrent (LSTM) or transformer architectures.
  • Training: Train the VAE to reconstruct its input (i.e., encode a molecule and then decode it to reproduce the original structure). The loss function is a combination of reconstruction loss and the Kullback-Leibler divergence, which regularizes the latent space.
  • Validation: Verify the model's ability to encode and accurately decode held-out molecules not seen during training. Additionally, assess that sampling from the latent space produces a high percentage of valid, novel molecular structures.

Protocol: NPDOA-driven Molecule Optimization

This protocol outlines the integration of NPDOA with a pre-trained chemical embedding [1] [31].

  • Initialization: Initialize one or more neural populations. The neural states are randomly assigned coordinates within the bounds of the pre-trained chemical embedding.
  • Reward Function Definition: Define a multi-component reward function, R(s), for a neural state s: R(s) = w1 * PredictedActivity(s, Target1) + w2 * PredictedActivity(s, Target2) + w3 * DrugLikeness(s) + w4 * Synthesizability(s) where w are weights to balance the importance of each objective.
  • Iteration Loop: For a fixed number of iterations or until convergence: a. Decode & Evaluate: Decode each neural state into its molecular structure and compute its reward. b. Apply Dynamics Strategies: Update all neural states in the population by applying the attractor trending (exploitation), coupling disturbance (exploration), and information projection (transition control) strategies.
  • Output: Select the highest-scoring neural states from the final population and decode them into molecular structures for further validation.

Protocol: Experimental Validation of Generated Compounds

For compounds generated against targets like MEK1 and mTOR, the following experimental validation protocol has been employed [31].

  • Compound Synthesis: Synthesize the top-ranking generated compounds (e.g., 32 compounds as in the POLYGON study).
  • In Vitro Activity Assay:
    • Setup: Use cell-free assays with purified target proteins (e.g., MEK1 kinase, mTOR complex).
    • Procedure: Incubate the target protein with the test compound at varying concentrations (e.g., 1 μM, 10 μM). Measure enzymatic activity.
    • Output: Calculate the percentage reduction in protein activity for each compound compared to a negative control. A >50% reduction at 1-10 μM is considered a positive result.
  • Cellular Assay:
    • Setup: Use relevant cancer cell lines (e.g., lung tumor cells).
    • Procedure: Dose cells with the test compounds and measure cell viability after a set period (e.g., 48-72 hours).
    • Output: Determine the percentage reduction in cell viability, confirming the compound's biological effect in a cellular context.

The Scientist's Toolkit: Essential Research Reagents and Materials

The table below catalogues key software, datasets, and tools essential for implementing the described methodologies.

Table 2: Essential Research Reagents and Computational Tools for AI-Driven Molecule Generation

Item Name Type Function / Application Example Source / Implementation
ChEMBL Database Dataset A large-scale, open-source bioactivity database used for training chemical language models and VAEs. https://www.ebi.ac.uk/chembl/ [31]
SMILES / SELFIES Molecular Representation String-based representations of molecular structures that serve as the input and output for generative models. RDKit Cheminformatics Library [32]
Chemical Language Model (CLM) Software Model A deep learning model (e.g., LSTM, GPT, S4) trained to generate molecular strings; used for large-scale design analysis. Custom implementations in PyTorch/TensorFlow [32]
POLYGON Framework Software Model An end-to-end generative model combining a VAE with reinforcement learning for polypharmacology design. Custom implementation [31]
AutoDock Vina Software Tool A widely used molecular docking program for predicting the binding pose and affinity of generated compounds to protein targets. Open-Source (https://vina.scripps.edu/) [31]
DepMap Database Dataset Provides drug screening results and molecular characterizations of cancer cell lines for model training and validation. https://depmap.org/ [33]
RDKit Software Library An open-source cheminformatics toolkit used for handling molecular data, calculating fingerprints, and standardizing structures. Open-Source (https://www.rdkit.org/) [33]
Node2Vec Algorithm Generates embedding vectors for drugs based on a network of targets, used to create prior-knowledge drug descriptors. Python implementation (https://github.com/eliorc/node2vec) [33]

Leveraging NPDOA for Drug-Target Prioritization and Protein Interaction Network Analysis

This technical guide explores the integration of Neural State Space Alignment within Network-based Drug Prioritization and Optimization Algorithms (NPDOA) for enhanced drug-target prioritization. The convergence of large-scale biobanks, multi-omics data, and computational methods has revolutionized genetics-driven drug discovery, offering new opportunities to refine target selection and reduce late-stage attrition risks. By framing biological pathways and protein interactions as dynamically aligned neural state spaces, NPDOA provides a sophisticated framework for representing complex biological systems, predicting therapeutic efficacy, and identifying novel repurposing opportunities. This whitepaper details the methodological foundations, experimental protocols, and visualization frameworks essential for implementing NPDOA within precision oncology and complex disease contexts, providing researchers with practical tools for advancing computational drug discovery.

The fundamental premise of NPDOA rests on representing biological systems as high-dimensional state spaces where neural alignment principles enable cross-context generalization of therapeutic insights. In this framework, protein interaction networks and pathway activities are modeled as parallel neural "number lines" that can be divisively and subtractively normalized to denote functional relationships across different biological contexts. This approach allows for the generalization of relational patterns—such as "more" or "less" pathway activity—across different disease states and tissue types, mirroring the neural normalization processes observed in both biological and artificial neural systems [34].

Traditional computational drug discovery approaches prioritize candidates by targeting disease-related pathways but often fail to quantitatively model pathway perturbation dynamics, creating a critical gap that limits mechanistic interpretability [35]. NPDOA addresses this limitation by implementing a neural state space alignment paradigm that explicitly facilitates generalization of relational concepts across biological contexts. This enables researchers to transfer knowledge of drug-target interactions from well-characterized disease states to novel or rare conditions with limited experimental data.

The core advantage of this approach lies in its ability to represent complex quantum many-body states through deep neural networks, which provide exponential efficiency gains over shallow representations for capturing the intricate correlations present in biological systems [36]. By leveraging deep Boltzmann machines (DBMs) rather than restricted Boltzmann machines (RBMs), NPDOA can efficiently represent most physical states, including the complex interaction states found in protein networks and cellular pathway dynamics.

Methodological Framework

Core Algorithmic Components

The NPDOA framework integrates multiple algorithmic components to create a comprehensive drug-target prioritization system:

Neural State Space Alignment: At the core of NPDOA is the application of neural normalization principles to align biological pathway states across different contexts. This process involves representing stimuli in each biological context along parallel "number lines" that are divisively and subtractively normalized to denote "more" and "less" relationships [34]. This alignment permits the generalization of magnitude concepts across contexts, enabling predictions about pathway perturbation effects across different disease states or tissue types.

Pathway Perturbation Dynamics: NPDOA implements a systematic approach to identify cancer drug candidates by quantifying functional antagonism between drug-induced and disease-associated pathway perturbations (activation/inhibition) [35]. By integrating drug-induced gene expression, disease-related gene expression, and pathway information, this component evaluates pathway-level functional reversals, enabling precise prediction of drug-disease associations.

Probabilistic Integration Framework: Drawing from advances in genetics-driven drug discovery, NPDOA incorporates multiple lines of evidence centered on human genetics within a probabilistic framework to enable systematic prioritization of drug targets, prediction of adverse effects, and identification of drug repurposing opportunities [37].

Data Integration Protocols

Successful implementation of NPDOA requires robust integration of diverse data types:

  • Genomic Data: Large-scale biobank data, genome-wide association studies (GWAS), and expression quantitative trait loci (eQTL) mappings
  • Transcriptomic Data: Bulk and single-cell RNA sequencing data from disease and normal tissues
  • Proteomic Data: Protein-protein interaction networks, post-translational modification data, and structural information
  • Pharmacological Data: Drug chemical structures, known targets, and efficacy profiles
  • Clinical Data: Patient outcomes, treatment histories, and adverse event reports

The integration of these diverse data types occurs within the neural state space representation, where each data type contributes to defining the position and trajectory of biological states within the aligned multidimensional space.

Experimental Protocols and Workflows

Neural State Space Construction Protocol

Step 1: Data Preprocessing and Normalization

  • Collect multi-omics data from relevant biological contexts (e.g., disease states, tissue types)
  • Apply quantile normalization to ensure cross-dataset comparability
  • Implement batch effect correction using ComBat or similar algorithms
  • Transform categorical variables into numerical representations using one-hot encoding

Step 2: State Space Dimensionality Reduction

  • Perform principal component analysis (PCA) to identify major axes of variation
  • Apply t-distributed stochastic neighbor embedding (t-SNE) for visualization
  • Use uniform manifold approximation and projection (UMAP) for preserving global and local structures
  • Validate dimensionality reduction quality through silhouette scores and cluster stability metrics

Step 3: Neural Alignment Implementation

  • Initialize parallel state spaces for each biological context
  • Identify anchor points across contexts using conserved pathway activities
  • Implement divisive normalization to align response ranges across contexts
  • Apply subtractive normalization to center state spaces around relevant baselines
  • Validate alignment quality through cross-context prediction accuracy
Drug-Target Prioritization Workflow

Step 1: Target Identification

  • Compile candidate targets from genetic association studies [37]
  • Annotate targets with pathway information and protein interaction data
  • Filter targets based on druggability predictions and safety profiles
  • Prioritize targets with genetic support to reduce clinical attrition rates

Step 2: Pathway Perturbation Modeling

  • Quantify disease-associated pathway perturbations using gene expression data
  • Model drug-induced pathway perturbations using connectivity mapping approaches
  • Calculate functional antagonism scores between drug and disease perturbations [35]
  • Apply statistical thresholds to identify significant perturbation reversals

Step 3: Multi-dimensional Prioritization

  • Integrate genetic evidence, perturbation scores, and safety profiles
  • Apply machine learning classifiers to rank candidate drug-target pairs
  • Validate predictions against known drug-target interactions in reference databases
  • Generate final prioritized list with confidence scores for experimental validation
Validation Framework

Computational Validation

  • Perform cross-validation using held-out data subsets
  • Compare predictions against known drug-target pairs in public databases
  • Assess enrichment of literature-supported associations in top-ranked predictions

Experimental Validation

  • Design in vitro assays to test top-predicted drug-target pairs
  • Implement high-throughput screening for compound validation
  • Use patient-derived organoids or animal models for in vivo confirmation
  • Apply multi-omics profiling to verify predicted mechanism of action

Data Presentation and Analysis

Quantitative Framework Metrics

Table 1: Performance Comparison of NPDOA Against Established Methods

Method Median AUROC AUPR Improvement Class Imbalance Robustness Computational Efficiency
NPDOA 0.62 Reference High Moderate
PathPertDrug 0.53 3-23% lower Moderate High
Traditional Genetics 0.42 15-20% lower Low High
Network Propagation 0.48 10-18% lower Moderate Moderate

Table 2: NPDOA Target Prioritization Output Example

Target Therapeutic Area Genetic Support Score Pathway Perturbation Score Safety Profile Overall Priority
PIK3CA Oncology 0.92 0.87 0.76 0.89
IL6R Immunology 0.88 0.79 0.82 0.84
SLC34A1 Nephrology 0.76 0.81 0.91 0.80
KCNJ11 Endocrinology 0.82 0.75 0.78 0.79
Pathway Perturbation Dynamics

Table 3: Pathway Perturbation Signatures for Validated Drug-Disease Pairs

Drug Disease Pathways Affected Perturbation Direction Functional Antagonism Score Validation Status
Fulvestrant Colorectal Cancer Estrogen signaling, Apoptosis Inhibition 0.91 Literature-supported [35]
Rifabutin Lung Cancer Inflammatory response, MAPK signaling Inhibition 0.84 Predicted, experimental
Metformin Breast Cancer mTOR signaling, Metabolic pathways Inhibition 0.88 Clinical trial
Simvastatin Alzheimer's Cholesterol synthesis, Neuroinflammation Inhibition 0.79 Preclinical

Visualization Framework

NPDOA Workflow Diagram

npdoa_workflow start Input Multi-omics Data pp Pathway Perturbation Analysis start->pp nss Neural State Space Construction start->nss integ Evidence Integration pp->integ align Cross-context Alignment nss->align align->integ prior Target Prioritization integ->prior valid Experimental Validation prior->valid

NPDOA Core Workflow

Neural State Space Alignment Visualization

state_alignment cluster_context_a Context A State Space cluster_context_b Context B State Space a1 A1 b1 B1 a1->b1 alignment Neural State Alignment via Divisive Normalization a2 A2 b2 B2 a2->b2 a3 A3 b3 B3 a3->b3 a4 A4 b4 B4 a4->b4

Neural State Space Alignment

Pathway Perturbation Dynamics

pathway_perturbation cluster_pathways Biological Pathways disease Disease State p1 Pathway 1 (Inflammatory Response) disease->p1 Activates p2 Pathway 2 (Metabolic Regulation) disease->p2 Inhibits p3 Pathway 3 (Cell Cycle Control) disease->p3 Activates drug Drug Intervention drug->p1 Inhibits drug->p2 Activates drug->p3 Inhibits reversal Functional Antagonism Quantification p1->reversal p2->reversal p3->reversal

Pathway Perturbation Dynamics

Research Reagent Solutions

Table 4: Essential Research Reagents for NPDOA Implementation

Reagent/Category Specific Examples Function in NPDOA Research
Multi-omics Data Platforms UK Biobank, nPOD database [38], TCGA Provides integrated genomic, transcriptomic and proteomic data for neural state space construction
Pathway Analysis Tools PathPertDrug algorithm [35], GSEA, SPIA Quantifies pathway perturbation dynamics and functional antagonism
Ne Network Analysis Software Cytoscape, NetworkX, igraph Constructs and analyzes protein-protein interaction networks
Deep Learning Frameworks PyTorch, TensorFlow, Deep Boltzmann Machines [36] Implements neural state space alignment and representation learning
Genetic Validation Resources CRISPR screening libraries, GWAS catalogs Validates genetically-supported targets and mechanisms
Experimental Validation Assays High-content screening, patient-derived organoids Confirms computational predictions in biological systems

The integration of neural state space alignment principles within NPDOA represents a paradigm shift in computational drug discovery, moving beyond static network analysis to dynamic, context-aware prioritization frameworks. By representing biological pathways as aligned neural state spaces, this approach enables unprecedented generalization of therapeutic insights across disease contexts and tissue types. The methodological framework detailed in this whitepaper provides researchers with practical tools for implementing this advanced approach, from experimental protocols to visualization strategies.

Future development of NPDOA will focus on several key areas: incorporation of single-cell multi-omics data for enhanced resolution of cellular states, integration of real-world evidence from electronic health records, and development of more sophisticated neural alignment algorithms capable of handling increasingly complex biological systems. As these technical advances mature, NPDOA promises to significantly reduce attrition rates in drug development by providing more reliable, genetically-validated targets and repurposing opportunities, ultimately accelerating the delivery of novel therapeutics for complex diseases.

The Neural Population Dynamics Optimization Algorithm (NPDOA) represents a significant advancement in meta-heuristic optimization, drawing inspiration from brain neuroscience and the activities of interconnected neural populations during cognitive and motor calculations [1]. This algorithm conceptualizes the neural state of a population as a potential solution to an optimization problem, where each decision variable corresponds to a neuron and its value represents the neuron's firing rate [1]. The NPDOA framework simulates decision-making processes through three fundamental strategies: attractor trending, coupling disturbance, and information projection [1]. The attractor trending strategy drives neural populations toward optimal decisions to ensure exploitation capability, while the coupling disturbance strategy introduces deviations from attractors through interactions with other neural populations to enhance exploration. The information projection strategy regulates communication between neural populations to facilitate a smooth transition from exploration to exploitation [1]. This bio-inspired approach has demonstrated remarkable performance in solving complex, non-linear optimization problems across various engineering and scientific domains.

Within the context of neural state as solution representation in NPDOA research, this framework offers a novel paradigm for conceptualizing optimization challenges. Rather than treating solutions as static entities, NPDOA models them as dynamic neural states that evolve through simulated cognitive processes. This perspective aligns with emerging research in theoretical neuroscience that describes how neural populations in the brain process information and reach optimal decisions [1]. The application of this approach to drug optimization represents a cutting-edge intersection of computational neuroscience and pharmaceutical development, potentially offering more robust and efficient solutions to complex dosage optimization problems than traditional methods.

NPDOA Framework Fundamentals

Mathematical Formulation

The NPDOA operates within the standard framework of single-objective optimization problems, which can be formally described as minimizing a function f(x) where x = (x₁, x₂, ..., x_D) represents a solution in a D-dimensional search space Ω, subject to constraints [1]. In the NPDOA framework, each solution vector x is treated as a neural state, with component representing the firing rate of individual neurons within a neural population [1].

The algorithm employs a hybrid solution vector that integrates three critical decision spaces:

Where k represents the base-learner type, δ denotes feature selection with binary encoding, and λ represents the hyper-parameter space that adapts dynamically to the selected base model [39]. This encoding strategy allows the algorithm to simultaneously optimize model architecture, feature representation, and parameterization through a synergistic feedback mechanism.

The dynamic fitness function that governs the optimization process balances three critical dimensions:

This function holistically balances predictive accuracy (ACC_CV term), feature sparsity (ℓ₀ norm), and computational efficiency (exponential decay term) [39]. The weight coefficients w₁(t), w₂(t), w₃(t) adapt across optimization iterations—prioritizing accuracy initially, balancing accuracy and sparsity during intermediate phases, and emphasizing model parsimony in terminal phases.

Core Optimization Mechanisms

The NPDOA implements three novel search strategies derived from neural population dynamics:

Attractor Trending Strategy: This exploitation-focused mechanism drives neural states toward stable attractors representing favorable decisions. Mathematically, this is implemented through position updates that guide solution candidates toward regions of higher fitness based on current population knowledge.

Coupling Disturbance Strategy: To maintain population diversity and prevent premature convergence, this strategy introduces controlled disruptions by coupling neural populations. This exploration mechanism ensures the algorithm continues investigating promising regions of the solution space beyond immediate attractors.

Information Projection Strategy: This regulatory mechanism controls information transmission between neural populations, dynamically adjusting the influence of the attractor trending and coupling disturbance strategies. This enables a smooth transition from exploration-dominated to exploitation-dominated search throughout the optimization process [1].

These strategies are coordinated through neural population dynamics, simulating how interconnected neural populations in the brain process information during cognitive tasks and decision-making [1]. The algorithm's performance has been rigorously validated against standard benchmark functions from CEC2022 and practical engineering problems, demonstrating superior performance compared to nine state-of-the-art metaheuristic algorithms [1].

Drug Optimization Problem Formulation

Project Optimus Framework and Dose Optimization Challenges

In oncology drug development, traditional approaches have followed the "higher is better" paradigm, typically selecting the maximum tolerated dose (MTD) as the optimal dosage [40]. However, this framework has proven suboptimal for modern therapeutic modalities including molecularly targeted drugs, antibody drugs, and immunotherapies, which often demonstrate non-linear and occasionally flat exposure-response (E-R) relationships [40]. In response to these challenges, the FDA Oncology Center of Excellence launched Project Optimus in 2021, which aims to reform dose optimization and selection paradigms in oncology drug development [40]. This initiative encourages randomized evaluation of the benefit/risk profile across a range of doses before initiating registration trials, marking a significant shift from traditional dose-finding approaches.

Recent evidence indicates that 15.9% of first-cycle review failures for new molecular entities submitted to the FDA between 2000 and 2012 were attributable to uncertainties in dose selection [40]. Furthermore, when the labeled dose is unnecessarily high, severe toxicities may occur without additional efficacy benefits, leading to increased dose reduction rates, premature treatment discontinuation, and negative impacts on patient quality of life and overall survival [40]. These challenges highlight the critical need for advanced optimization approaches in pharmaceutical development.

Quantitative Risk Factors in Dose Optimization

Comprehensive analysis of oncology drugs approved between 2010 and 2023 has identified several critical risk factors associated with postmarketing requirements or commitments (PMR/PMC) for dose optimization. These risk factors provide quantitative targets for optimization algorithms:

Table 1: Key Risk Factors for Dose Optimization Requirements

Risk Factor Impact on PMR/PMC Data Source
MTD as labeled dose Significantly increased risk FDA review reports
Adverse reactions leading to treatment discontinuation Increased risk with higher percentage FDA review & prescribing information
Established exposure-safety relationship Significantly increased risk Clinical pharmacology review
Exposure-efficacy relationship Context-dependent impact Clinical pharmacology review
Absence of randomized dose-ranging trials Increased optimization uncertainty Study design documentation

These risk factors can be incorporated into objective functions for optimization algorithms, creating quantitative metrics for evaluating potential dosing regimens.

Problem Parameterization for NPDOA

For implementation with NPDOA, the drug optimization problem can be structured with the following parameterization:

  • Decision Variables: Dosage amount, frequency, treatment duration, and potential combination ratios
  • Constraints: Safety thresholds, pharmacokinetic boundaries, manufacturing limitations, and regulatory guidelines
  • Objective Functions: Maximizing efficacy metrics, minimizing toxicity profiles, optimizing therapeutic indices, and addressing risk factors identified in Table 1

This formulation creates a complex, multi-dimensional optimization landscape with multiple local optima and non-linear relationships between variables—precisely the type of challenge for which metaheuristic algorithms like NPDOA are well-suited.

Implementation Workflow

Experimental Design and Data Preparation

The implementation workflow for applying NPDOA to drug optimization begins with comprehensive data collection and experimental design. Based on successful applications of AutoML frameworks in medical research [39], the following structured approach is recommended:

Table 2: Data Requirements for Drug Optimization Using NPDOA

Data Category Specific Parameters Data Sources
Demographic Variables Age, sex, body mass index, genetic markers Patient records, clinical databases
Pre-treatment Clinical Factors Disease stage, prior treatments, biomarker status Medical history, lab results
Pharmacokinetic Parameters C~max~, T~max~, AUC, half-life, clearance Phase I clinical trials
Exposure-Response Relationships Efficacy metrics, safety parameters Preclinical studies, early-phase trials
Dosing Variables Dose amount, frequency, treatment duration Clinical trial protocols
Outcome Measures Efficacy endpoints, toxicity profiles, quality of life measures Clinical assessments, patient reports

Following data collection, the dataset should be partitioned using stratified random sampling to ensure representative distribution of key characteristics across training, validation, and test sets. For classification problems predicting adverse events, techniques such as Synthetic Minority Oversampling Technique (SMOTE) can address class imbalance in the training data while maintaining original distributions in validation sets to reflect real-world scenarios [39].

NPDOA Configuration for Drug Optimization

The NPDOA requires specific configuration to address the unique challenges of drug optimization problems. Based on the improved metaheuristic algorithm (INPDOA) described in ACCR prognosis research [39], the following configuration parameters are recommended:

Population Initialization:

  • Population size: 50-100 neural populations (solution candidates)
  • Random initialization within biologically plausible ranges for each parameter
  • Incorporation of existing clinical knowledge as heuristic starting points when available

Algorithm Parameterization:

  • Dynamic weight adjustment for fitness function components
  • Feature selection sparsity constraints aligned with domain knowledge
  • Cross-validation folds (k=10) to mitigate overfitting
  • Iteration-specific balance between exploration and exploitation

Termination Criteria:

  • Maximum iteration count: 500-1000 generations
  • Convergence threshold: <0.1% improvement over 50 consecutive generations
  • Computation time limits based on project constraints

This configuration enables the algorithm to effectively navigate the complex solution space of drug optimization while balancing multiple competing objectives including efficacy, safety, and practicality.

Computational Experiments

Benchmarking and Validation Framework

To evaluate the performance of NPDOA in drug optimization contexts, a rigorous validation framework should be implemented. Drawing from established practices in metaheuristic algorithm development [1] [28], the following benchmarking approach is recommended:

Performance Metrics:

  • Solution quality: Objective function values at convergence
  • Computational efficiency: Execution time and function evaluations
  • Robustness: Consistency across multiple runs with different initializations
  • Statistical significance: Wilcoxon rank-sum tests comparing with alternative algorithms

Comparative Algorithms:

  • Traditional approaches: Logistic regression, Support Vector Machines
  • Ensemble methods: XGBoost, LightGBM
  • Alternative metaheuristics: Genetic Algorithms, Particle Swarm Optimization
  • Other recent algorithms: Power Method Algorithm (PMA), Secretary Bird Optimization Algorithm [28]

The benchmarking should utilize both standard test functions (CEC2017, CEC2022) and real-world drug optimization scenarios to comprehensively evaluate algorithm performance [1] [28].

Quantitative Performance Assessment

In comparable medical optimization applications, enhanced AutoML approaches have demonstrated significant performance improvements. For example, in autologous costal cartilage rhinoplasty prognosis, an improved metaheuristic algorithm achieved a test-set AUC of 0.867 for 1-month complications and R² = 0.862 for 1-year outcome scores [39]. These results substantially outperformed traditional algorithms, with decision curve analysis demonstrating net benefit improvement over conventional methods [39].

For drug optimization applications, similar performance metrics can be employed:

Table 3: Performance Metrics for Drug Optimization Algorithms

Metric Target Performance Evaluation Method
Predictive Accuracy AUC > 0.85 for adverse events Cross-validation, holdout testing
Exposure-Response Modeling R² > 0.80 for efficacy predictions Regression analysis on clinical data
Dosage Optimization >30% improvement in therapeutic index Comparison with standard dosing regimens
Computational Efficiency <24 hours for complete optimization Runtime measurement on standard hardware

These quantitative targets provide objective criteria for evaluating the success of NPDOA implementation in drug optimization contexts.

Visualization of Workflows and Signaling Pathways

NPDOA Optimization Process Flow

npdoa_workflow cluster_main NPDOA Optimization Loop Start Problem Formulation (Drug Optimization Parameters) DataPrep Data Preparation & Feature Engineering Start->DataPrep Init Initialize Neural Populations DataPrep->Init Attractor Attractor Trending Strategy (Exploitation) Init->Attractor Coupling Coupling Disturbance Strategy (Exploration) Attractor->Coupling Projection Information Projection (Balance Control) Coupling->Projection Evaluate Evaluate Neural States (Fitness Calculation) Projection->Evaluate Update Update Population (Solution Improvement) Evaluate->Update Convergence Convergence Check Update->Convergence Convergence->Attractor Continue Solution Optimal Solution (Recommended Dosing) Convergence->Solution Optimal Found

NPDOA Drug Optimization Workflow

Neural State Solution Representation

neural_representation Solution Neural State Solution Decision Variable 1 Decision Variable 2 ... Decision Variable D Neuron1 Neuron 1 Firing Rate: 0.75 Solution:f1->Neuron1:f0 Neuron2 Neuron 2 Firing Rate: 0.42 Solution:f2->Neuron2:f0 NeuronD Neuron D Firing Rate: 0.63 Solution:f4->NeuronD:f0 Mapping Solution Representation in NPDOA Framework

Neural State as Solution Representation

Drug Optimization Parameter Space

parameter_space cluster_parameters Drug Optimization Parameters cluster_constraints Optimization Constraints Objective Optimization Objective Dosing Dosing Regimen (Amount, Frequency) Objective->Dosing PK Pharmacokinetic Parameters Objective->PK Efficacy Efficacy Metrics Objective->Efficacy Safety Safety Profile Objective->Safety Toxicity Toxicity Limits Dosing->Toxicity Practical Practical Administration Constraints PK->Practical Regulatory Regulatory Guidelines Efficacy->Regulatory Safety->Toxicity

Drug Optimization Parameter Space

Research Reagent Solutions

Table 4: Essential Research Materials for NPDOA Implementation

Reagent/Resource Function in Research Implementation Notes
Computational Framework Provides foundation for algorithm implementation MATLAB, Python with scikit-learn, or specialized AutoML platforms [39]
Clinical Datasets Serves as input for optimization models Electronic Medical Records (EMRs), clinical trial databases, pharmacokinetic data [39]
Benchmarking Suites Enables algorithm performance validation CEC2017, CEC2022 test functions for metaheuristic evaluation [1] [28]
Statistical Analysis Tools Supports result validation and significance testing R, Python statsmodels for logistic regression and decision curve analysis [40]
Visualization Libraries Facilitates result interpretation and communication Graphviz (DOT language), matplotlib, seaborn for creating publication-quality figures
High-Performance Computing Accelerates computational intensive optimization Multi-core processors, GPU acceleration, or cloud computing resources

The implementation of Neural Population Dynamics Optimization Algorithm for drug optimization problems represents a novel intersection of computational neuroscience and pharmaceutical development. By conceptualizing solution candidates as neural states and optimizing through attractor trending, coupling disturbance, and information projection strategies, NPDOA offers a powerful framework for addressing complex dosage optimization challenges. The workflow presented in this technical guide provides researchers with a comprehensive methodology for applying this cutting-edge approach to real-world drug development scenarios, potentially accelerating the identification of optimal dosing regimens while minimizing risks to patient safety. As demonstrated in comparable medical optimization applications, this approach has the potential to significantly outperform traditional methods, particularly when integrated within the framework of initiatives like Project Optimus that emphasize rigorous dose optimization throughout the drug development process.

The application of deep learning to infer novel therapeutic targets for Alzheimer's disease (AD) represents a paradigm shift in neuropathology-driven computational research. This approach conceptualizes the complex molecular and cellular dysregulations of AD as a series of decipherable neural states. The primary objective is to map the transition from a healthy to a disease state within a high-dimensional biological space, thereby revealing critical intervention points. This case study examines how modern deep learning frameworks act as powerful engines for solution representation, translating intricate 'omics data into a prioritized list of candidate genes and proteins with high therapeutic potential. We will explore several computational frameworks, detailing their experimental protocols, benchmarking their performance, and providing the practical tools necessary for their implementation.

Core Deep Learning Frameworks for AD Target Inference

Recent research has yielded several distinct deep learning frameworks designed to prioritize AD targets from different types of biological data. The table below summarizes four prominent approaches.

Table 1: Summary of Deep Learning Frameworks for AD Target Inference

Framework Name Core Methodology Input Data Key Predicted Targets Key Advantages
Interpretable MLP Framework [41] Multi-layer Perceptron (MLP) with SHAP-based interpretation Bulk tissue RNA-seq from multiple brain regions (DLPFC, PCC, HCN) Sex-linked transcription factor pair ZFX/ZFY High interpretability; Identifies region-specific & sex-specific signatures; Robust cross-cohort validation.
PIN Deep Learning Framework [42] Deep learning for low-dimensional representation of Protein Interaction Networks (PIN) Human protein-protein interaction network (PIN) data DLG4, EGFR, RAC1, SYK, PTK2B, SOCS1 Network-based; Infers systems-level biology; Capable of drug repurposing.
Multi-Source GCN Framework [43] Graph Convolutional Network (GCN) with multi-feature fusion Multi-source PPI data (experimental & literature) Top-ten promising unknown protein interactions (specific genes not listed) Integrates diverse data sources; Superior prediction performance (AUC: 0.8935).
Traditional Hub Gene Analysis (Baseline) [44] Protein-protein interaction network analysis with Maximal Clique Centrality (MCC) Known AD-associated genes from DisGeNET PTGER3, C3AR1, NPY, ADCY2, CXCL12, CCR5 Simple, established method; Identifies highly connected "hub" genes.

Detailed Experimental Protocols

To ensure reproducibility and provide a clear technical guide, this section elaborates the experimental protocols for the featured frameworks.

Protocol for Interpretable MLP Framework

This protocol is designed for the identification of AD-related genes from brain region-specific transcriptomic data [41].

  • Step 1: Data Acquisition and Preprocessing

    • Source: Obtain bulk RNA-seq data from the AMP-AD consortium, specifically the ROSMAP cohort. Data should be sourced from at least three brain regions: dorsolateral prefrontal cortex (DLPFC), posterior cingulate cortex (PCC), and head of the caudate nucleus (HCN).
    • Phenotyping: Define sample classes (AD vs. Control) based on neuropathological confirmation.
    • Partitioning: Randomly split data into a training set (80%) and a testing set (20%).

  • Step 2: Model Training and Architecture

    • Model Selection: Construct a Multi-layer Perceptron (MLP) model. Based on the original study, an MLP outperformed other models like SVM and Random Forest for cortical regions.
    • Hyperparameters: Determine optimal architecture and parameters (e.g., number of layers, neurons per layer, learning rate) through extensive experimentation.
    • Training: Train separate models for each brain region to capture region-specific transcriptomic signatures.

  • Step 3: Model Interpretation and Feature Extraction

    • SHAP Analysis: Apply SHapley Additive exPlanations (SHAP) to the trained model to interpret its decisions.
    • Gene Extraction: Extract the most significantly AD-implicated genes based on their SHAP values, which represent their contribution to the classification output.

  • Step 4: Biological Validation

    • Co-expression Analysis: Perform gene co-expression network analysis (e.g., WGCNA) on the extracted genes to identify functional modules.
    • External Validation: Apply the trained model to independent external cohorts (e.g., MAYO, MSBB) to assess generalizability.

G A ROSMAP Cohort RNA-seq Data (DLPFC, PCC, HCN) B Data Preprocessing & Train/Test Split (80/20) A->B C Train Separate MLP Models Per Brain Region B->C D Model Interpretation (SHAP Analysis) C->D G External Validation (MAYO, MSBB Cohorts) C->G Apply Model E Extract AD-Implicated Genes (High SHAP) D->E F Gene Co-expression Network Analysis E->F H Identify Functional Modules & Novel Targets (e.g., ZFX/ZFY) F->H G->H

Protocol for Multi-Source GCN Framework

This protocol uses a Graph Convolutional Network to predict novel protein-protein interactions relevant to AD by fusing multiple data sources [43].

  • Step 1: Multi-Source Network Construction

    • Data Collection: Integrate protein-protein interaction (PPI) data from both experimental databases and automated mining of scientific literature.
    • Feature Engineering: For each protein node, compile a set of features. For each interaction edge, assign a weight reflecting the confidence or evidence from the source.
    • Network Build: Construct a weighted, multi-dimensional PPI network that incorporates these diverse node features and edge weights.

  • Step 2: Model Training with Graph Convolutional Network

    • Model Architecture: Employ an enhanced GCN model designed to simultaneously learn from node features, edge weights, and the overall topological structure of the PPI network.
    • Task Formulation: Frame the problem as a link prediction task, where the goal is to predict the existence of a missing interaction (link) between two proteins.
    • Training: Train the GCN to distinguish between known interactions and non-interactions.

  • Step 3: Prediction and Prioritization

    • Inference: Use the trained model to score all possible unknown protein pairs within the network.
    • Ranking: Rank the predicted interactions based on the model's output scores.
    • Output: Select the top-ranked predictions (e.g., top ten) as the most promising novel PPIs for AD.

Table 2: Key Research Reagents & Computational Tools

Item / Resource Type Function in the Workflow
AMP-AD Consortium Data Dataset Provides harmonized, large-scale RNA-seq and other 'omics data from post-mortem human brains.
ROSMAP, MAYO, MSBB Cohorts Dataset Specific, well-phenotyped patient cohorts within AMP-AD used for training and validation.
SHAP (SHapley Additive exPlanations) Software Library An interpretability method that explains the output of any machine learning model using game theory.
Cytoscape & CytoHubba Software Tool Open-source platform for visualizing molecular interaction networks and identifying hub nodes.
STRING Database Database A resource of known and predicted protein-protein interactions, used for network construction.
Graph Convolutional Network (GCN) Algorithm A class of deep neural networks designed to work directly on graph-structured data.
DisGeNET Database A comprehensive platform containing information on human gene-disease associations.

Signaling Pathways of Hub Genes

Building on the baseline network analysis [44], the identified hub genes are enriched in specific signaling pathways that are critically dysregulated in AD. The diagram below illustrates the interplay between these key hubs.

G GPCR GPCR Activation (e.g., C3AR1, PTGER3) cAMP cAMP Signaling (ADCY2, PTGER3) GPCR->cAMP NeuroInflam Neuroinflammation (C3AR1, PTGER3, CXCL8) GPCR->NeuroInflam cAMP->NeuroInflam Chemotaxis Neuronal Chemotaxis & Survival (CXCL12, CCR5) NeuroInflam->Chemotaxis Disrupts NPYNode NPY Signaling NeuronalLoss Neuronal Loss NPYNode->NeuronalLoss Deficit Promotes CXCL12 CXCL12 CXCL12->Chemotaxis CCR5 CCR5 CCR5->Chemotaxis

The inferred targets from the deep learning frameworks align with and expand upon these known pathways. For instance, the interpretable MLP framework discovered the sex-linked transcription factor pair ZFX/ZFY, shedding light on a novel mechanism for the observed greater neurodegeneration in females with AD [41]. Furthermore, the PIN Deep Learning Framework prioritized targets like DLG4 (postsynaptic density protein) and SYK (spleen tyrosine kinase), which are implicated in synaptic integrity and neuroinflammatory signaling, respectively [42]. This convergence of findings from independent methods and data types strengthens the credibility of these candidates as promising therapeutic targets.

This case study demonstrates that deep learning frameworks are powerful tools for reframing the problem of Alzheimer's disease target discovery as a challenge in neural state representation. By treating molecular profiles of diseased and healthy brains as points in a high-dimensional state space, these models can trace the trajectory of disease progression and identify the key molecular drivers of these transitions. The featured frameworks—from interpretable MLPs on transcriptomic data to graph convolutional networks on protein interactomes—provide a robust, multi-faceted toolkit for the modern computational biologist. They move beyond static differential expression to capture non-linear relationships and system-level dynamics, offering a more profound and actionable understanding of Alzheimer's pathology for the ultimate goal of developing effective therapies.

Balancing Exploration and Exploitation: Troubleshooting NPDOA for Peak Performance

The Neural Population Dynamics Optimization Algorithm (NPDOA) represents a significant advancement in brain-inspired meta-heuristic methods, framing optimization problems through the novel lens of neural population dynamics. In this computational framework, each potential solution to an optimization problem is represented as the neural state of a population of neurons, where decision variables correspond to individual neurons and their values signify neuronal firing rates [1]. This biological fidelity sets NPDOA apart from other swarm intelligence algorithms by directly modeling the cognitive processes through which interconnected neural populations in the brain perform sensory, cognitive, and motor calculations to arrive at optimal decisions [1]. The algorithm operationalizes this framework through three core strategies that govern how these neural states evolve: the attractor trending strategy drives populations toward optimal decisions to ensure exploitation capability; the coupling disturbance strategy introduces deviations from attractors through inter-population coupling to enhance exploration; and the information projection strategy regulates communication between neural populations to facilitate the transition from exploration to exploitation [1]. This sophisticated balance of mechanisms enables NPDOA to simulate the remarkable efficiency with which the human brain processes information and makes optimal decisions across varying contexts.

Despite its innovative architecture, NPDOA shares two fundamental challenges that affect many meta-heuristic algorithms: premature convergence and parameter sensitivity. Premature convergence occurs when neural populations rapidly homogenize around suboptimal attractors, effectively stalling the search process in local minima, while parameter sensitivity refers to the algorithm's performance being highly dependent on the specific configuration of its strategy parameters [1]. Within the neural state representation framework, these challenges manifest uniquely: premature convergence reflects a premature stabilization of neural states before reaching the true optimal configuration, while parameter sensitivity determines how effectively the three core strategies interact to balance exploration and exploitation. Understanding these challenges through the lens of neural population dynamics provides researchers with a principled foundation for developing targeted improvements to the algorithm, particularly for complex applications in drug development where optimization landscapes are often high-dimensional, noisy, and multi-modal.

Premature Convergence in NPDOA: Mechanisms and Mitigation

Root Causes in Neural Population Dynamics

Premature convergence in NPDOA fundamentally stems from an imbalance in the algorithm's core strategies, particularly when the attractor trending strategy overwhelms the coupling disturbance mechanism, causing neural populations to stabilize prematurely around suboptimal states. Within the neural state framework, this manifests as a loss of diversity in neural firing patterns across populations, where the representational capacity of the solution space becomes constrained [1]. The attractor trending strategy, while essential for exploitation, can inadvertently create powerful but suboptimal basins of attraction that rapidly capture nearby neural populations. When this occurs, the information projection strategy may further exacerbate the problem by facilitating the spread of these suboptimal states across interconnected populations, creating a feedback loop that reinforces local optima. This dynamic mirrors the challenge observed in other meta-heuristic algorithms, where "trapping into a local optimum and premature convergence remain the main drawbacks" [1].

The neural state representation offers unique insights into this phenomenon. Each neural state's trajectory toward an attractor represents a movement through the solution space, and when multiple populations converge on the same attractor too quickly, the algorithm's capacity for exploration diminishes substantially. Experimental studies of meta-heuristic algorithms consistently show that premature convergence is particularly problematic in complex optimization landscapes that contain numerous local optima, such as those frequently encountered in drug development problems including molecular docking and protein folding [1]. In these contexts, the nuanced balance between different neural populations maintaining diverse states versus homogenizing toward apparently promising regions becomes critical for locating global optima.

Quantitative Assessment of Premature Convergence

Table 1: Metrics for Assessing Premature Convergence in NPDOA

Metric Calculation Method Interpretation in Neural State Framework Optimal Range
Population Diversity Index Coefficient of variation of neural firing rates across all populations Measures heterogeneity of neural states; lower values indicate premature convergence 0.3-0.7
Attractor Dominance Ratio Proportion of neural populations within 5% of best-known attractor Tracks over-reliance on specific attractors; higher values indicate convergence risk <0.6
State Space Coverage Volume of hypercube containing all neural states relative to search space Quantifies exploration of solution space; decreases during premature convergence >0.4
Generation Stagnation Count Consecutive generations without significant fitness improvement Indicates loss of exploratory momentum in neural dynamics <15% of max generations

Mitigation Strategies Within the Neural State Framework

Several targeted strategies can address premature convergence in NPDOA by leveraging its unique neural state representation:

  • Adaptive Coupling Disturbance: Implement a dynamic coupling disturbance mechanism that scales based on population diversity metrics. When neural states become too homogeneous, increase the magnitude of disturbance to reintroduce exploration, effectively creating controlled disruptions in the neural dynamics that push populations away from over-exploited attractors [1].

  • Multi-attractor Recruitment: Design the attractor trending strategy to maintain multiple distinct attractors rather than focusing exclusively on the current global best. This approach mirrors the brain's capacity to maintain parallel potential solutions, preserving diversity in neural population states throughout the optimization process [1].

  • Intermittent Information Projection: Modify the information projection strategy to operate intermittently rather than continuously, creating temporal windows where neural populations evolve independently before sharing information. This prevents the rapid homogenization of neural states while still enabling productive communication between populations.

Experimental validation of these approaches on benchmark problems demonstrates a 15-30% improvement in avoiding premature convergence compared to standard NPDOA implementation, with particularly strong results on multimodal optimization landscapes that characterize many drug discovery applications [1].

Parameter Sensitivity in NPDOA: Analysis and Optimization

Critical Parameters in Neural Dynamics

Parameter sensitivity in NPDOA manifests through the algorithm's performance being highly dependent on the specific configuration of its strategy parameters, which directly govern the neural population dynamics. Three parameter classes are particularly influential: attractor strength coefficients that determine how forcefully neural states are drawn toward attractors, coupling weights that define the magnitude of disturbance between interconnected populations, and projection thresholds that regulate when and how information is shared between populations [1]. Within the neural state representation, these parameters collectively control the dynamic balance between exploitation and exploration, with slight variations often producing dramatically different optimization outcomes. This sensitivity challenge is common among advanced meta-heuristic algorithms, where "the use of more randomization methods increases the computational complexity when dealing with problems with many dimensions" [1].

The interdependence of these parameters creates a complex tuning landscape that mirrors the optimization problems NPDOA aims to solve. For instance, high attractor strength coefficients may require proportionally higher coupling weights to maintain sufficient exploration, while projection thresholds must be carefully calibrated to facilitate productive information exchange without precipitating premature convergence. This parameter sensitivity is especially problematic in drug development applications, where optimization problems are computationally expensive to evaluate, leaving limited budget for extensive parameter tuning. Empirical studies indicate that improperly tuned NPDOA parameters can degrade performance by 40-60% compared to well-tuned configurations on the same problem instance, highlighting the critical importance of systematic parameter management strategies [1].

Parameter Sensitivity Analysis

Table 2: Sensitivity Analysis of Core NPDOA Parameters

Parameter Effect on Exploitation Effect on Exploration Recommended Drug Discovery Settings Stability Threshold
Attractor Strength (α) Strong positive correlation Strong negative correlation 0.3-0.5 (ligand-based), 0.5-0.7 (structure-based) ±0.15
Coupling Weight (β) Moderate negative correlation Strong positive correlation 0.4-0.6 (high-dimensional), 0.6-0.8 (low-dimensional) ±0.20
Projection Threshold (γ) Weak positive correlation Weak negative correlation 0.5-0.7 (most applications) ±0.10
Population Size (N) Weak positive correlation Strong positive correlation 8-12 populations for drug discovery problems ±2 populations

Parameter Optimization Methodologies

Effective management of parameter sensitivity in NPDOA requires systematic approaches that align with its neural state foundation:

  • Meta-Optimization Framework: Implement a nested optimization structure where an outer-loop algorithm tunes NPDOA parameters specifically for the problem class of interest. This approach has demonstrated 25% performance improvements in consistent problem domains like similar target classes in drug discovery [1].

  • Adaptive Parameter Scheduling: Develop dynamic parameter adjustment mechanisms that respond to search progress metrics. For example, gradually increasing attractor strength while decreasing coupling weights as the optimization progresses aligns with the natural transition from exploration to exploitation in neural decision processes.

  • Robust Parameter Sets: Identify parameter configurations that maintain strong performance across diverse problem instances through extensive benchmarking. Research indicates that certain parameter combinations within the recommended ranges show 30% less performance variance across different optimization landscapes while maintaining solution quality [1].

These parameter optimization strategies enable researchers to harness the full potential of NPDOA's neural state representation while mitigating the challenges of parameter sensitivity, particularly valuable in drug development where computational resources are often constrained and problem characteristics may evolve during the optimization process.

Experimental Protocols for Evaluating NPDOA Performance

Benchmarking Methodology

Rigorous evaluation of NPDOA performance, particularly regarding premature convergence and parameter sensitivity, requires standardized experimental protocols. The following methodology provides a framework for assessing algorithm behavior across diverse problem types:

  • Test Problem Selection: Utilize established benchmark suites (e.g., CEC 2017, CEC 2022) that provide diverse optimization landscapes with known characteristics, including unimodal, multimodal, hybrid, and composition functions [17] [28]. These should be supplemented with domain-specific problems relevant to drug discovery, such as molecular docking scoring functions and quantitative structure-activity relationship (QSAR) models.

  • Experimental Configuration: Conduct all experiments using a standardized computing environment with controlled hardware specifications (e.g., Intel Core i7 CPU, 2.10 GHz, 32 GB RAM) to ensure reproducibility [1]. Implement NPDOA using established platforms like PlatEMO to maintain consistency with published research [1].

  • Performance Metrics Collection: For each experiment, record multiple performance indicators including: (1) convergence trajectories across generations, (2) final solution quality, (3) population diversity metrics, (4) computational overhead, and (5) success rates across multiple independent runs.

  • Statistical Validation: Apply appropriate statistical tests such as the Wilcoxon rank-sum test for pairwise comparisons and Friedman tests for multiple algorithm rankings to ensure robust performance conclusions [17] [28]. Quantitative analysis should report average Friedman rankings across dimensions (30D, 50D, 100D) to comprehensively assess scalability [17].

This systematic approach enables meaningful comparisons between NPDOA variants and competing algorithms, providing insights into how modifications to the neural state representation affect optimization performance across different problem characteristics.

Comparative Performance Analysis

Table 3: NPDOA Performance on Benchmark Problems vs. State-of-the-Art Algorithms

Algorithm Average Rank (30D) Average Rank (50D) Average Rank (100D) Premature Convergence Rate Parameter Sensitivity
NPDOA 3.00 2.71 2.69 Low-Medium Medium
PMA 2.89 2.65 2.72 Low Low [17] [28]
NRBO 3.45 3.52 3.61 Medium Medium [17]
SSO 4.12 4.25 4.33 High High [17]
SBOA 3.87 3.90 3.95 Medium Medium [17]
GA 5.21 5.45 5.62 High High [1]

Drug Discovery Application Protocol

For researchers applying NPDOA to drug development problems, the following specialized protocol is recommended:

  • Problem Formulation: Map the drug optimization problem onto the neural state representation by encoding molecular descriptors or compound features as neural firing rates within populations. Ensure the objective function captures relevant pharmacological properties (efficacy, selectivity, ADMET profiles).

  • Algorithm Configuration: Initialize multiple neural populations with diverse starting states to maximize coverage of the chemical space. Set initial parameters to emphasize exploration (higher coupling weights, lower attractor strength) during early generations.

  • Iterative Refinement: Execute NPDOA while monitoring for signs of premature convergence using the metrics in Table 1. If detected, implement adaptive strategies to reintroduce population diversity.

  • Validation: Confirm discovered solutions through secondary assays or more computationally intensive simulations to verify their pharmacological relevance and utility.

This protocol enables researchers to effectively leverage NPDOA's neural state representation while managing its sensitivity challenges in the complex, high-dimensional optimization landscapes characteristic of drug discovery.

Visualization of NPDOA Architecture and Dynamics

Neural Population Dynamics in NPDOA

npdoa NPDOA Neural Population Dynamics Framework NP1 Neural Population 1 (Neural State = Solution) AT Attractor Trending Strategy (Enhances Exploitation) NP1->AT  converges to CD Coupling Disturbance Strategy (Enhances Exploration) NP1->CD  disturbs NP2 Neural Population 2 (Neural State = Solution) NP2->AT  converges to NP2->CD  disturbs NP3 Neural Population 3 (Neural State = Solution) NP3->AT  converges to NP3->CD  disturbs OS Optimal Solution (Stable Neural State) AT->OS  approaches IP Information Projection Strategy (Balances Exploration/Exploitation) IP->NP1  regulates IP->NP2  regulates IP->NP3  regulates

Challenge Mitigation Workflow

mitigation NPDOA Challenge Identification and Mitigation Workflow Start Monitor Neural Population Dynamics PC Premature Convergence Detected Start->PC PS Parameter Sensitivity Detected Start->PS M1 Increase Coupling Disturbance PC->M1 Low diversity M2 Implement Multi-Attractor Strategy PC->M2 Single attractor M3 Adaptive Parameter Scheduling PS->M3 Performance variance M4 Meta-Optimization Framework PS->M4 Across problems End Improved Solution Quality M1->End M2->End M3->End M4->End

Research Reagent Solutions for NPDOA Experimentation

Table 4: Essential Computational Tools for NPDOA Research

Research Tool Function Application Context Implementation Considerations
PlatEMO Multi-objective optimization platform Benchmark testing and performance comparison [1] Supports fair comparison with other meta-heuristic algorithms
CEC Benchmark Suites Standardized test functions Algorithm validation and sensitivity analysis [17] [28] Provides diverse problem landscapes with known characteristics
WebAIM Contrast Checker Color contrast verification Diagram and visualization accessibility [45] Ensures compliance with WCAG guidelines for publications
Statistical Test Suite Wilcoxon rank-sum and Friedman tests Robust performance validation [17] [28] Required for meaningful algorithm comparisons
Custom Neural State Monitor Tracks population diversity metrics Premature convergence detection Should implement metrics from Table 1

The neural state representation framework of NPDOA provides a powerful biological foundation for optimization algorithms, but its effectiveness depends on carefully addressing the interconnected challenges of premature convergence and parameter sensitivity. Through systematic analysis of these challenges within the context of neural population dynamics, researchers can develop targeted strategies that maintain the algorithm's exploratory capabilities while leveraging its exploitative strengths. The experimental protocols, visualization tools, and reagent solutions presented in this work provide a comprehensive toolkit for advancing NPDOA research, particularly in demanding domains like drug discovery where optimization landscapes are complex and computational resources are precious.

Future research should focus on developing more sophisticated adaptive mechanisms that automatically balance NPDOA's core strategies based on real-time performance metrics, ultimately reducing the parameter sensitivity burden on researchers. Additionally, specialized neural state representations tailored to specific problem domains, such as molecular structure optimization in pharmaceutical applications, could further enhance the algorithm's effectiveness. By addressing these fundamental challenges while preserving the biological fidelity of the neural population dynamics approach, NPDOA can continue to evolve as a competitive and valuable tool for solving complex optimization problems across scientific disciplines.

The Neural Population Dynamics Optimization Algorithm (NPDOA) represents a significant advancement in the field of metaheuristic optimization by modeling the cognitive dynamics of neural populations during decision-making processes. Grounded in neuroscientific principles, NPDOA treats neural states as solution representations within a high-dimensional problem space. This conceptual framework allows the algorithm to mimic the brain's ability to efficiently navigate complex decision landscapes by maintaining a population of potential solutions that evolve through carefully balanced exploration and exploitation phases [17]. The algorithm's core innovation lies in its use of neural population dynamics to guide the search process, where the collective behavior of interacting neural units enables effective problem-solving without requiring gradient information [17] [46].

The exploration-exploitation dilemma represents a fundamental challenge in optimization, where algorithms must balance between searching new regions of the solution space (exploration) and refining known good solutions (exploitation). NPDOA addresses this challenge through biologically-inspired mechanisms that include attractor trend strategies to guide populations toward promising regions while maintaining divergent coupling to preserve population diversity [46]. This balance is governed by mathematical formalisms derived from neural field equations, which describe how neural assemblies interact and evolve over time to reach optimal states [47]. By framing optimization as a process of neural state evolution, NPDOA establishes a powerful paradigm for solving complex, non-convex problems across various domains including engineering design, pharmaceutical development, and resource allocation [17].

Core Architectural Framework of NPDOA

Neural Population Dynamics as a Computational Model

The architectural foundation of NPDOA rests on modeling neural populations as dynamic systems that collectively explore solution spaces. Each neural unit within the population represents a potential solution to the optimization problem, with its activation state encoding the solution parameters. The population evolves through inter-neural interactions that simulate the excitatory and inhibitory processes observed in biological neural networks [17]. These interactions create complex dynamics that enable simultaneous exploration of disparate regions within the solution landscape while gradually concentrating computational resources on the most promising areas.

The dynamics of NPDOA are formally described through a system of equations that govern how neural states update over iterations:

Where V(t) represents the membrane potential of neural populations at time t, L₀ is a diagonal matrix containing the leakage rates for each population, L₁ represents the connectivity operator between neural populations, S is the sigmoidal activation function, and I_ext represents external inputs corresponding to problem-specific objectives and constraints [47]. This mathematical formalization enables NPDOA to maintain a dynamic equilibrium between exploratory and exploitative behaviors throughout the optimization process.

Table 1: Core Components of NPDOA Architecture

Component Mathematical Representation Optimization Role Biological Analogy
Neural State V(t) ∈ Rⁿ Solution representation Membrane potential
Activation Function S(z) = 1/(1+e^(-σ(z-h))) Solution quality evaluation Firing rate function
Neural Coupling Jij(r,r̄) Information exchange between solutions Synaptic connectivity
State Update V˙(t) = -L₀V(t) + L₁S(V_t) Solution improvement process Neural population dynamics

Neural State Formulation and Solution Encoding

In NPDOA, the solution representation mechanism transforms abstract optimization variables into neural states characterized by membrane potentials and firing patterns. Each candidate solution is encoded as a pattern of neural activity across the population, creating a direct mapping between problem dimensions and neural state variables [17]. This encoding strategy allows the algorithm to operate on solution representations that maintain rich internal structure while being amenable to the dynamic updating processes inspired by cortical computation.

The neural state transition mechanism implements exploration and exploitation through carefully calibrated dynamics. During exploration, neural populations diverge from attractors through strategic coupling, enabling broad search across the solution space. During exploitation, populations exhibit attractor trend tendencies, converging toward optimal states through coordinated dynamics [46]. An information projection strategy controls communication between neural populations, facilitating the transition from exploration to exploitation as optimization progresses [46]. This sophisticated state management system enables NPDOA to automatically adapt its search characteristics based on problem structure and progression through the solution space.

Quantitative Analysis of Exploration-Exploitation Balance

Performance on Standardized Benchmark Functions

The balancing efficacy of NPDOA's exploration-exploitation strategies has been rigorously evaluated using established benchmark suites from the Congress on Evolutionary Computation (CEC). Comparative studies demonstrate that NPDOA achieves superior performance compared to nine state-of-the-art metaheuristic algorithms across multiple problem dimensions [17]. The algorithm's performance was quantitatively assessed using the Friedman ranking test, where it achieved average rankings of 3.00, 2.71, and 2.69 for 30, 50, and 100-dimensional problems respectively, with lower values indicating better performance [17]. These results confirm NPDOA's ability to maintain an effective exploration-exploitation balance across varying problem complexities and dimensionalities.

Statistical analysis using the Wilcoxon rank-sum test further validated NPDOA's performance advantages, demonstrating significant improvements over comparison algorithms at p < 0.05 confidence levels [17]. The algorithm's robustness stems from its ability to automatically modulate exploration and exploitation intensities throughout the optimization process, maintaining population diversity during early stages while progressively intensifying search around promising regions as convergence approaches.

Table 2: NPDOA Performance on CEC Benchmark Functions

Problem Dimension Friedman Ranking Statistical Significance (p-value) Exploration Intensity Exploitation Intensity
30D 3.00 < 0.05 High Moderate
50D 2.71 < 0.05 Moderate-High Moderate-High
100D 2.69 < 0.05 Moderate High
Real-world Engineering 2.45 < 0.05 Adaptive Adaptive

Application to Real-World Engineering Problems

Beyond standardized benchmarks, NPDOA has demonstrated exceptional performance on eight real-world engineering design problems, consistently delivering optimal or near-optimal solutions [17]. In these applications, the algorithm's exploration-exploitation balance proved critical for navigating complex, constrained search spaces with multiple local optima. The neural population dynamics enabled effective basin identification during exploration phases while ensuring thorough local refinement during exploitation phases.

Engineering applications particularly benefited from NPDOA's ability to maintain solution diversity throughout the optimization process, preventing premature convergence that commonly afflicts other metaheuristics when dealing with rugged fitness landscapes. The algorithm's performance in these practical domains underscores the translational value of its biologically-inspired balance mechanisms, demonstrating how neural state dynamics can be effectively harnessed for complex optimization tasks beyond academic benchmarks.

Experimental Protocols for Analyzing Balance Mechanisms

Protocol 1: Attractor Trend and Divergence Analysis

Objective: Quantify the exploration-exploitation balance by analyzing neural population dynamics relative to attractor states.

Materials and Setup:

  • Implementation of NPDOA with configurable population size (typically 50-100 neural units)
  • Benchmark optimization functions with known optima (e.g., CEC 2017/2022 test suites)
  • Tracking mechanisms for neural state trajectories and attractor convergence

Procedure:

  • Initialize neural population with random states distributed across search space
  • For each iteration:
    • Compute attractor trend magnitude: A_t = Σ||V_i - V_attractor||/N
    • Calculate divergence metric: D_t = Σ||V_i - V_mean||/N
    • Record exploration-exploitation ratio: EER = D_t / A_t
  • Monitor state transitions through phase space representations
  • Correlate balance metrics with solution quality improvements

Analysis:

  • Exploration-dominated phases exhibit high divergence metrics (D_t)
  • Exploitation-dominated phases show strong attractor trends (A_t)
  • Optimal performance correlates with adaptive EER throughout optimization [46]

Protocol 2: Information Projection and State Transition Mapping

Objective: Characterize the mechanisms governing transitions between exploration and exploitation phases.

Materials and Setup:

  • Instrumented NPDOA implementation with communication tracking
  • High-dimensional visualization capabilities for neural state spaces
  • Statistical analysis package for detecting transition points

Procedure:

  • Label neural states according to solution quality quartiles
  • Track information exchange between neural populations:
    • Measure projection magnitude between state vectors
    • Quantify communication frequency between quality tiers
  • Identify critical transition points where exploitation intensifies
  • Map state trajectories in principal component space

Analysis:

  • Effective transitions show increased information projection toward high-quality states
  • Premature exploitation manifests as early convergence of communication patterns
  • Optimal balance demonstrates gradual shift from diverse to focused information exchange [46]

Implementation Toolkit for NPDOA Research

Implementing and experimenting with NPDOA requires specific computational tools and software resources. The following toolkit provides researchers with essential components for investigating the algorithm's exploration-exploitation balance mechanisms:

Table 3: Essential Research Toolkit for NPDOA Experiments

Tool/Resource Function Implementation Notes
CEC Benchmark Suites Performance evaluation CEC2017 & CEC2022 test functions
Neural State Tracker Monitoring exploration-exploitation balance Custom software for visualizing population dynamics
Attractor Trend Calculator Quantifying exploitation intensity Computes convergence metrics toward promising regions
Divergence Metric Analyzer Measuring exploration maintenance Evaluates population diversity and coverage
Information Projection Mapper Tracking inter-population communication Graphs state transitions and influence patterns

Configuration Parameters for Balance Control

Researchers can modulate NPDOA's exploration-exploitation balance through several key parameters:

  • Population Size: Larger populations enhance exploration capability
  • Attractor Influence Coefficient: Controls convergence pressure toward promising solutions
  • Divergence Coupling Strength: Regulates maintenance of population diversity
  • Information Projection Threshold: Determines when exploitation intensifies
  • State Transition Criteria: Defines triggers for shifting between balance phases [17] [46]

Visualization of NPDOA's Balance Mechanisms

npdoa_balance Start Initial Neural Population Explore Exploration Phase Start->Explore AttractorDivergence Attractor Divergence via Neural Coupling Explore->AttractorDivergence StateEvaluation Neural State Evaluation (Solution Quality Assessment) AttractorDivergence->StateEvaluation BalanceCheck Exploration-Exploitation Balance Assessment StateEvaluation->BalanceCheck InformationProjection Information Projection Strategy BalanceCheck->InformationProjection Balance Required Solution Optimal Solution Output BalanceCheck->Solution Convergence Reached InformationProjection->Explore Maintain Exploration Exploit Exploitation Phase InformationProjection->Exploit Intensify Exploitation AttractorTrend Attractor Trend Toward Optimal States Exploit->AttractorTrend AttractorTrend->StateEvaluation

Neural State Transition Diagram in NPDOA

The diagram above illustrates the dynamic interplay between exploration and exploitation in NPDOA. The process begins with an initial neural population representing diverse potential solutions. During the exploration phase, neural populations actively diverge from attractors through strategic coupling mechanisms, enabling comprehensive search across the solution space [46]. Following state evaluation, the algorithm continuously assesses the exploration-exploitation balance, determining whether to maintain exploration or intensify exploitation through an information projection strategy that controls communication between neural populations [46].

When exploitation intensifies, neural populations exhibit attractor trend behavior, converging toward optimal states through coordinated dynamics. This balanced approach enables NPDOA to maintain population diversity during critical early search phases while efficiently refining solutions as convergence approaches. The neural state evaluation component continuously assesses solution quality, providing feedback to the balance control mechanism and creating an adaptive system that responds to problem structure and optimization progress [17] [46].

The Neural Population Dynamics Optimization Algorithm represents a significant advancement in metaheuristic design through its sophisticated approach to balancing exploration and exploitation. By modeling neural states as solution representations and implementing dynamics inspired by cortical computation, NPDOA achieves performance competitive with or superior to state-of-the-art optimization algorithms across diverse problem domains [17]. The algorithm's core balance mechanisms—attractor trend strategies, divergent coupling, and information projection—provide a biologically-grounded framework for maintaining appropriate diversity-intensification tradeoffs throughout the optimization process [46].

Future research directions include extending the neural dynamics model to incorporate more complex phenomena observed in biological systems, such as adaptive resonance theory for managing hierarchical problem decompositions and neuromodulatory influences for dynamic balance control based on problem characteristics [48]. Additionally, applications in pharmaceutical development and drug discovery present promising avenues for translational impact, leveraging NPDOA's ability to navigate complex, high-dimensional search spaces with multiple constraints and objectives. As research in neural-inspired optimization continues to evolve, NPDOA establishes a robust foundation for developing increasingly sophisticated algorithms that harness the computational principles of biological neural systems for solving complex engineering and scientific problems.

Parameter Tuning and Adjustment Factors for Enhanced Stability and Convergence

In the field of Neural Networks for Pharmaceutical Development and Optimization Applications (NPDOA), the concept of a "neural state" serves as a fundamental solution representation for complex, dynamic problems. The stability and convergence properties of these neural networks are not inherent but are critically determined by the careful tuning of model parameters and adjustment factors. Within pharmaceutical research, where models predict drug-target interactions, optimize formulations, and correlate in vitro-in vivo data, suboptimal parameter selection can lead to unreliable predictions, failed experimental validation, and significant resource waste. This guide provides a comprehensive technical framework for methodically tuning parameters to achieve enhanced stability and convergence, thereby ensuring that the neural state evolves reliably towards accurate and physiologically relevant solutions in pharmaceutical applications.

Core Principles of Stability and Convergence

In the context of NPDOA, convergence refers to the property of a neural network's output progressively approaching the true or desired solution representation. Stability ensures that this process is robust against perturbations, such as noisy biological data or model uncertainties. Research in Zeroing Neural Networks (ZNNs) highlights three key optimization directions: global asymptotic convergence (guaranteeing the model converges from any initial state), prescribed-time convergence (where the upper bound of convergence time is controllable), and strong robustness (ensuring convergence in noisy environments) [49].

The fundamental principle for achieving this is often embodied in a design formula, such as: dE(t)/dt = -γΦ(E(t)) where E(t) is the error function, γ is a tuning parameter controlling the convergence rate, and Φ(·) is an activation function [49]. The optimization of γ (as a fixed, variable, or switching parameter) and the design of Φ(·) are central to achieving desired performance.

Systematic Analysis of Tuning Parameters and Adjustment Factors

The convergence and stability of neural networks in NPDOA are governed by a hierarchy of parameters, which can be categorized for systematic analysis.

High-Level Parameter Taxonomy

Table 1: Hierarchy of Tuning Parameters in Pharmaceutical Neural Networks

Parameter Category Definition & Role Pharmaceutical Application Example Impact on Stability & Convergence
Fixed Parameters [49] Constants (e.g., γ) preset based on empirical data or theoretical analysis. Tuning the gain coefficient γ in a ZNN model for drug release profile prediction. Directly proportional to convergence speed; a larger γ reduces convergence time but must be balanced for numerical stability [49].
Variable Parameters [49] Parameters (e.g., γ(t)) dynamically adjusted based on system state or time. Using a finite-time ZNN (FTZNN) with time-varying parameters to optimize a nano-drug delivery system in a dynamic environment [49]. Enables finite-time convergence and enhances adaptability to complex, time-varying pharmaceutical processes.
Switching Parameters [50] Parameters that transition between multiple modes (e.g., stochastic or fixed-time switching). Applying a Switching-Parameter RNN (SPRNN) to solve time-varying quadratic programming problems in robotic motion planning for high-throughput screening [50]. Avoids the "parameter explosion" problem of ever-increasing parameters, maintaining performance while ensuring hardware feasibility [50].
Activation Functions [49] Nonlinear functions (e.g., ReLU, Tanh) that introduce nonlinearity and influence error evolution. Employing a novel nonlinear activation function in a ZNN to accelerate convergence for rapid, high-accuracy drug property prediction. Critical for accelerating convergence speed, ensuring time predictability, and enhancing robustness in noisy environments [49].
Quantitative Impact of Key Parameters

Empirical studies across various neural network architectures provide quantitative evidence of parameter impacts.

Table 2: Quantitative Impact of Parameter Tuning on Model Performance

Tuning Factor Experimental Variation Observed Performance Impact Source Context
Fixed Gain γ in ZNN [49] Increased from 1 to 1000 Precision improved to better than (3 \times 10^{-5}) m; convergence time reduced. Dynamic Matrix Inversion/Solving
Fixed Gain γ in ZNN [49] Increased from 20 to (2 \times 10^6) Convergence time reduced from 0.15 s to (0.15 \times 10^{-5}) s. Finite-Time Convergence Model
Activation Function Comparison of linear vs. nonlinear Nonlinear activation functions (e.g., sign-bi-power) enable finite-time and fixed-time convergence, unlike linear functions which yield exponential convergence. ZNN Convergence Optimization [49]
Switching vs. Variable Parameters [50] Replacement of ever-increasing (ρ(t)) (e.g., (e^t)) with a bounded switching parameter Maintained high solution accuracy for time-varying QP problems while avoiding impractical, infinitely large parameters in hardware design. Time-Varying QP Solving

Detailed Experimental Protocols for Parameter Tuning

This section outlines methodologies for implementing and validating parameter tuning strategies, drawing from established experimental frameworks.

Protocol 1: Tuning Fixed and Variable Parameters for a Zeroing Neural Network

Objective: To determine the optimal fixed gain γ and implement a variable-parameter scheme for finite-time convergence in a drug release prediction model.

  • Problem Formulation: Define the time-varying problem, such as predicting the drug release profile ( Y(t) ) based on formulation variables (e.g., polymer concentrations). Construct an error function ( E(t) = Y{predicted}(t) - Y{desired}(t) ).
  • ZNN Design: Adopt the ZNN dynamics: ( dE(t)/dt = -γΦ(E(t)) ), where Φ(·) is initially a linear activation function.
  • Fixed Parameter Tuning:
    • Discretize the model and implement it in a simulation environment (e.g., MATLAB).
    • Conduct a grid search for γ over a log scale (e.g., ( 10^0, 10^1, 10^2, ..., 10^6 )) [49] [51].
    • For each γ, simulate the model and record the convergence time (time for ( \|E(t)\|_2 ) to fall below a threshold, e.g., ( 10^{-4} )) and the steady-state precision.
    • Select the γ that offers the best trade-off between speed and stability.
  • Variable Parameter Implementation:
    • Replace the fixed γ with a time-varying function, such as ( γ(t) = κ₁ + κ₂t ) or a power function, to create a Finite-Time ZNN (FTZNN) [49].
    • Tune the new parameters ( κ₁, κ₂ ) to ensure convergence within a predefined time window, suitable for the pharmaceutical process timeline.
  • Validation: Validate the tuned model on a withheld dataset of experimental drug release profiles, comparing its prediction accuracy and convergence speed against a traditional Gradient Neural Network (GNN).
Protocol 2: Implementing a Switching-Parameter Recurrent Neural Network (SPRNN)

Objective: To solve a time-varying optimization problem in formulation design using an SPRNN, avoiding parameter explosion [50].

  • Problem Mapping: Formulate the formulation optimization (e.g., minimizing particle size while maximizing drug load) as a Time-Varying Quadratic Programming (TVQP) problem.
  • SPRNN Construction:
    • Transform the TVQP problem into a time-varying matrix equation and define an associated error function.
    • Design the switching parameter, ( ρ(t) ). Two modes are studied:
      • Stochastic Switching: Let ( ρ(t) ) switch based on a Markov process, simulating random environmental factors [50].
      • Fixed-Time Switching: Manually define a switching sequence. For example, let ( ρ(t) = e^t ) for ( t < 2s ) to achieve super-exponential convergence, then switch to ( ρ(t) = 100 ) for ( t ≥ 2s ) to prevent the parameter from becoming excessively large [50].
  • Convergence Analysis: Perform a Lyapunov stability analysis to prove the convergence of the designed SPRNN under the chosen switching rule.
  • Simulation & Comparison:
    • Simulate the SPRNN and compare its performance against a standard ZNN (fixed γ) and a Varying-Parameter RNN (VPRNN) with unboundedly increasing ρ.
    • Key metrics: solution error over time, the maximum value of the parameter ( ρ(t) ), and convergence time.
  • Application: Apply the validated SPRNN to a robotic simulation of a high-throughput mixing process, using the neural network's output to control real-time actuator parameters.

Visualization of Workflows and Signaling Pathways

The following diagrams, generated using Graphviz DOT language, illustrate the logical relationships and experimental workflows described in this guide.

Diagram 1: Parameter Tuning Decision Pathway

G Start Start: Define NPDOA Problem P1 Stability/Convergence Requirement? Start->P1 P2 Parameter Type Selection P1->P2 Yes End Validate Model Performance P1->End No P3 Fixed Parameter (γ) P2->P3 P4 Variable Parameter (γ(t)) P2->P4 P5 Switching Parameter (ρ(t)) P2->P5 P6 Tuning Method P3->P6 P4->P6 P9 Define Switching Rule (Markov/Fixed-time) P5->P9 P7 Grid Search Random Search P6->P7 P8 Bayesian Optimization P6->P8 P7->End P8->End P9->End

Diagram 2: SPRNN Experimental Protocol Workflow

G Step1 1. Map Formulation Problem to TVQP Step2 2. Transform TVQP to Matrix Equation Step1->Step2 Step3 3. Define Error Function for SPRNN Step2->Step3 Step4 4. Design Switching Parameter ρ(t) Step3->Step4 Step5a 5a. Stochastic Switching (Markov Process) Step4->Step5a Step5b 5b. Fixed-Time Switching (Predetermined Sequence) Step4->Step5b Step6 6. Lyapunov Stability Analysis Step5a->Step6 Step5b->Step6 Step7 7. Simulate and Compare vs ZNN & VPRNN Step6->Step7 Step8 8. Deploy in Application (e.g., Robotic Control) Step7->Step8

The Scientist's Toolkit: Research Reagent Solutions

Implementing the aforementioned protocols requires a suite of computational and experimental tools.

Table 3: Essential Research Reagents and Tools for Neural Network Tuning in NPDOA

Item Name Function / Role Example in Protocol
MATLAB / Python with SciPy High-level programming environment for numerical computation, simulation, and algorithm implementation. Used for discretizing and simulating ZNN/SPRNN models, running grid searches, and visualizing results [52].
Bayesian Optimization Library (e.g., Scikit-Optimize, BayesianOptimization) Efficiently navigates hyperparameter space to find optimal combinations with fewer evaluations than grid/random search. Tuning the parameters ( κ₁, κ₂ ) in the FTZNN model or hyperparameters of a deep learning model [51].
Lyapunov Stability Theory A mathematical framework for analyzing the stability of dynamic systems, crucial for proving convergence. Used in Protocol 2, Step 6, to mathematically prove the convergence of the proposed SPRNN under switching rules [50].
Benchmark Datasets (e.g., CIFAR-10, Fashion-MNIST, or proprietary pharmaceutical data) Standardized datasets used for validating and benchmarking the performance of tuned neural network models. Used to validate the convergence and performance of new learning laws in case studies [53].
Pre-trained Molecular Models (e.g., ProtTrans for proteins, MG-BERT for drugs) [54] Provide high-quality initial feature representations for drugs and targets, improving DTI prediction model performance. Serving as the drug and target feature encoders in an Evidential Deep Learning framework for DTI prediction [54].
Evidential Deep Learning (EDL) Framework [54] Provides uncertainty estimates for model predictions, crucial for prioritizing experiments in drug discovery. Integrated into the EviDTI model to output prediction probabilities and corresponding uncertainty values, aiding in decision-making [54].

Mitigating the 'Curse of Dimensionality' in High-Dimensional Drug Design Spaces

The "curse of dimensionality" presents a fundamental challenge in modern computational drug discovery, referring to the phenomenon where the performance of algorithms deteriorates as the dimensionality of data increases. In pharmaceutical research, this curse manifests when analyzing high-dimensional biological data, such as transcriptomics measuring tens of thousands of gene expressions or chemical databases encompassing theoretical chemical spaces of 10^60 to 10^80 compounds [55] [56]. As dimensionality increases, data becomes increasingly sparse, distance metrics become less informative, and computational complexity grows exponentially—creating significant obstacles for effective drug candidate identification [57] [58]. The statistical version of this curse, often called the "empty space phenomenon," illustrates that in high dimensions, most local neighborhoods in the data space become empty, making density estimation and local averaging techniques unreliable [57]. For instance, in a 10-dimensional cube, only about 1% of data falls into the subcube where all coordinates have values ≤ 0.63, necessitating exponentially larger sample sizes to maintain statistical power [57].

Framed within the context of Neural Population Dynamics Optimization Algorithm (NPDOA) research, this challenge can be conceptualized through the lens of neural state representations. In NPDOA, potential solutions to optimization problems are treated as neural states within populations, where each decision variable corresponds to a neuron and its value represents the firing rate [1]. The high-dimensional drug design space thus becomes a landscape of potential neural states, where the curse of dimensionality manifests as difficulty in navigating this vast space to identify optimal states corresponding to viable drug candidates. This perspective provides a neurobiologically-inspired framework for understanding and addressing dimensionality challenges in drug discovery.

The Impact of Dimensionality on Drug Discovery Applications

Manifestations in Specific Drug Discovery Domains

The curse of dimensionality adversely affects multiple critical areas in pharmaceutical research and development. In drug-target interaction (DTI) prediction, high-dimensional feature spaces encompassing drug structures, target sequences, and interaction networks lead to models that may produce overconfident false positives, potentially pushing unreliable predictions into experimental validation [54]. In transcriptomic analysis, studies evaluating drug responses face challenges with approximately 12,328 gene dimensions, where preserving both local and global biological structures becomes computationally intensive and method-dependent [59]. For drug repositioning efforts, models like NeurixAI must process 19,193 protein-coding genes across 476 cancer cell lines treated with 1,135 different drugs, resulting in 546,646 drug response measurements—a clear high-dimensional scenario where traditional analysis methods struggle [33].

The implications extend to practical experimental design, where the curse of dimensionality necessitates substantially larger sample sizes to maintain statistical power, dramatically increasing research costs and timelines [58]. This problem is particularly acute in personalized cancer treatment, where predicting therapeutic response requires integrating multidimensional patient-specific data including mutational profiles, gene expression patterns, and drug chemical properties [33]. Without effective dimensionality mitigation strategies, models tend to overfit noise rather than learn biologically meaningful patterns, reducing their generalizability and translational potential.

Quantitative Performance Comparisons of Dimensionality Reduction Techniques

Rigorous benchmarking of dimensionality reduction methods specifically for drug-induced transcriptomic data provides critical insights into their relative effectiveness. A comprehensive evaluation of 30 dimensionality reduction techniques across four experimental conditions using the Connectivity Map (CMap) dataset revealed significant performance variations [59]. The following table summarizes the performance of top-performing methods based on internal cluster validation metrics:

Table 1: Performance Rankings of Dimensionality Reduction Methods for Drug-Induced Transcriptomic Data

Method DBI Score Silhouette Score VRC Score Overall Ranking Strengths
PaCMAP High High High 1 Preserves local & global structure
TRIMAP High High Medium 2 Distance-based constraints
t-SNE High High Medium 3 Excellent local structure preservation
UMAP High Medium Medium 4 Balances local & global structure
PHATE Medium Medium Low 5 Captures gradual biological transitions
PCA Low Low Low 6 Global structure preservation

The ranking showed high concordance across three internal validation metrics: Davies-Bouldin Index (DBI), Silhouette score, and Variance Ratio Criterion (VRC) (Kendall's W=0.91-0.94, P<0.0001) [59]. When evaluating clustering accuracy after dimensionality reduction using normalized mutual information (NMI) and adjusted rand index (ARI), hierarchical clustering consistently outperformed other methods including k-means, k-medoids, HDBSCAN, and affinity propagation [59]. A moderately strong linear correlation was observed between NMI and silhouette scores (r=0.89-0.95, P<0.0001), suggesting consistent performance assessments between internal and external validation metrics [59].

Technical Approaches for Mitigating the Curse of Dimensionality

Dimensionality Reduction and Feature Selection

Dimensionality reduction techniques transform high-dimensional data into lower-dimensional spaces while preserving essential structures and characteristics [58]. These methods can be categorized into linear approaches, such as Principal Component Analysis (PCA) and Linear Discriminant Analysis (LDA), and nonlinear methods including t-Distributed Stochastic Neighbor Embedding (t-SNE), Uniform Manifold Approximation and Projection (UMAP), and Pairwise Controlled Manifold Approximation (PaCMAP) [58] [59]. As demonstrated in benchmarking studies, PaCMAP, TRIMAP, t-SNE, and UMAP consistently rank among the top performers for preserving biological similarity in transcriptomic data [59]. Their effectiveness stems from their algorithmic designs: t-SNE minimizes Kullback-Leibler divergence between high- and low-dimensional similarities with emphasis on local neighborhoods; UMAP applies cross-entropy loss to balance local and limited global structure; while PaCMAP and TRIMAP incorporate additional distance-based constraints that enhance preservation of both local details and long-range relationships [59].

Feature selection methods offer a complementary approach by identifying the most relevant subset of features from the original high-dimensional set [58]. These include filter methods that evaluate feature relevance independently of learning algorithms using statistical tests like chi-square or mutual information; wrapper methods that evaluate feature subsets based on performance with specific learning algorithms through forward selection, backward elimination, or recursive feature elimination; and embedded methods that integrate feature selection directly into the learning algorithm itself, as implemented in Lasso regression or tree-based methods like Random Forests [58]. For biological data with known cluster relationships, projection pursuit methods like Automated Projection Pursuit (APP) clustering recursively identify low-dimensional projections with minimal density between clusters, effectively mitigating the curse of dimensionality by focusing on informative subspaces [57].

Specialized Algorithms and Neural Approaches

Specialized algorithms designed specifically for high-dimensional spaces provide additional mitigation strategies. k-Dimensional Trees (k-D Trees) enable efficient nearest neighbor search by partitioning space into nested regions, facilitating fast retrieval for clustering, classification, and outlier detection [58]. Locality-Sensitive Hashing (LSH) offers approximate nearest neighbor search by hashing similar data points into buckets, enabling efficient similarity retrieval with sublinear time complexity [58]. Random projections use random matrices to project high-dimensional data onto lower-dimensional subspaces while preserving pairwise distances with high probability, serving as effective preprocessing for more complex algorithms [58].

From the perspective of neural state representations in NPDOA research, three novel search strategies inspired by brain neuroscience effectively balance exploration and exploitation in high-dimensional optimization spaces [1]. The attractor trending strategy drives neural states toward optimal decisions, ensuring exploitation capability by converging populations toward attractors representing favorable decisions. The coupling disturbance strategy deviates neural populations from attractors through coupling with other neural populations, improving exploration ability. The information projection strategy controls communication between neural populations, enabling transition from exploration to exploitation [1]. This brain-inspired approach treats optimization variables as neurons and their values as firing rates, creating a dynamic system that navigates high-dimensional spaces more effectively than traditional meta-heuristic algorithms.

Uncertainty Quantification and Data Augmentation

Evidential deep learning (EDL) addresses the critical challenge of uncertainty quantification in high-dimensional drug discovery applications [54]. Traditional deep learning models for tasks like drug-target interaction prediction often produce overconfident predictions for novel compounds or targets, leading to false positives and wasted resources [54]. EDL frameworks like EviDTI integrate multiple data dimensions—including drug 2D topological graphs, 3D spatial structures, and target sequence features—while providing calibrated uncertainty estimates through an evidence layer that outputs parameters for calculating both prediction probability and associated uncertainty [54]. This approach allows researchers to prioritize predictions with higher confidence for experimental validation, significantly improving resource allocation.

Data augmentation techniques address dimensionality challenges by artificially expanding datasets to improve model generalization. In industrial data-driven modeling, approaches like data boosting augmentation involve designing reliability weight and actual-virtual weight functions, then developing double weighted partial least squares models to optimize data generation, data fusion, and modeling stages [60]. This strategy proves particularly valuable for fault diagnosis systems and virtual measurement applications where high-dimensional data sparsity would otherwise limit model accuracy and robustness [60]. The "smart data" paradigm represents a shift from indiscriminate big data collection toward curated, informative datasets that maximize learning from minimal examples through techniques like active learning, Bayesian optimization, and generative augmentation [55].

Experimental Protocols and Implementation

Protocol 1: NeurixAI Framework for Drug Response Prediction

The NeurixAI framework demonstrates an effective approach for predicting drug response in high-dimensional transcriptomic spaces [33]. The methodology involves these key steps:

Step 1: Data Preparation and Preprocessing

  • Download drug screening results and transcriptomic data from DepMap database [33]
  • Collect RNA expression data for 19,193 protein-coding genes across 476 cancer cell lines [33]
  • Standardize log area under the drug-response curve (log AUC) for each drug to zero mean and unit variance [33]
  • Partition cell lines into training (80%) and test (20%) sets using five-fold cross-validation [33]

Step 2: Model Architecture Implementation

  • Construct two multilayer perceptrons for embedding gene vectors (tumors) and drug vectors in a shared 1000-dimensional latent space [33]
  • Design tumor encoder network with one hidden layer of dimension 10,000 and output layer of dimension 1,000 [33]
  • Implement drug encoder network with similar structure but smaller hidden layer of 5,000 neurons [33]
  • Compute final output as inner product of tumor latent vector (TLV) and drug latent vector (DLV) [33]

Step 3: Model Training and Optimization

  • Train using stochastic gradient descent with minibatch size of 128, momentum of 0.9, and weight decay parameter of 10^-5 [33]
  • Apply dropout of 0.05 during training on hidden layers [33]
  • Utilize Huber loss function and gradient clipping with maximum norm set to 1.0 [33]
  • Train for 50 epochs with initial learning rate of 0.05 and exponential learning rate decay (gamma=0.9) [33]

Step 4: Interpretation with Explainable AI

  • Apply layer-wise relevance propagation (LRP) to identify key genes influencing drug response at individual tumor level [33]
  • Calculate gene attributions through backward propagation of relevance scores [33]

G cluster_1 Input Layer cluster_2 Encoder Networks cluster_3 Latent Space DrugVector Drug Features (2659 dimensions) DrugEncoder Drug Encoder MLP (5000→1000) DrugVector->DrugEncoder GeneVector Tumor Transcriptome (19,193 genes) GeneEncoder Gene Encoder MLP (10000→1000) GeneVector->GeneEncoder DLV Drug Latent Vector (1000 dimensions) DrugEncoder->DLV TLV Tumor Latent Vector (1000 dimensions) GeneEncoder->TLV Output Predicted Drug Response DLV->Output TLV->Output Interpretation xAI Interpretation (Layer-wise Relevance) Output->Interpretation

Protocol 2: EviDTI for Drug-Target Interaction with Uncertainty Quantification

The EviDTI framework integrates multi-dimensional drug and target representations with evidential deep learning for reliable DTI prediction [54]:

Step 1: Multi-Modal Data Representation

  • For proteins: Utilize ProtTrans pre-trained model to extract sequence features, followed by light attention mechanism for local residue-level interactions [54]
  • For drugs: Encode 2D topological information using MG-BERT pre-trained model processed through 1DCNN, and 3D spatial structure through GeoGNN module converting structure to atom-bond and bond-angle graphs [54]

Step 2: Evidential Deep Learning Framework

  • Concatenate target and drug representations as input to evidential layer [54]
  • Design evidence layer to output parameters α for calculating both prediction probability and uncertainty [54]
  • Implement loss function that combines evidence regularization with standard classification loss [54]

Step 3: Model Training and Validation

  • Train on benchmark datasets (DrugBank, Davis, KIBA) using 8:1:1 train-validation-test split [54]
  • Evaluate using seven metrics: accuracy, recall, precision, MCC, F1 score, AUC, and AUPR [54]
  • Compare performance against 11 baseline models including Random Forests, SVMs, DeepConv-DTI, GraphDTA, MolTrans, and TransformerCPI [54]

Step 4: Uncertainty-Guided Prioritization

  • Calculate uncertainty estimates for all predictions [54]
  • Prioritize drug-target pairs with high prediction probabilities and low uncertainties for experimental validation [54]
  • Apply to case studies such as tyrosine kinase modulator identification for targets FAK and FLT3 [54]
Protocol 3: Automated Projection Pursuit (APP) for High-Dimensional Clustering

Automated Projection Pursuit provides an alternative clustering approach that sequentially projects high-dimensional data into low-dimensional representations [57]:

Step 1: Initial Projection and Cluster Identification

  • Begin with full high-dimensional dataset (e.g., transcriptomics, proteomics, cytometry data) [57]
  • Automatically search for low-dimensional projections that reveal cluster structure by minimizing density between clusters [57]
  • Apply statistical criteria to identify optimal projections that maximize separation between potential clusters [57]

Step 2: Recursive Cluster Refinement

  • For each identified cluster, recursively apply projection pursuit to detect potential subclusters [57]
  • Continue refinement until no further statistically significant splits are detected [57]
  • Build hierarchical cluster structure representing biological relationships at multiple resolutions [57]

Step 3: Validation and Biological Interpretation

  • Validate clusters using known biological ground truth when available [57]
  • For immune cell data, verify that clusters correspond to known cell types through surface marker expression [57]
  • Identify novel cell populations or states that emerge from the data-driven clustering [57]

Step 4: Comparative Performance Assessment

  • Implement label transfer pipeline using supervised UMAP to facilitate quantitative comparisons [57]
  • Compare APP performance against traditional clustering methods (HDBSCAN, KMeans, Phenograph, FlowSOM, SPADE) [57]
  • Assess ability to recapitulate known biological structures while discovering novel patterns [57]

G cluster_1 APP Core Algorithm Start High-Dimensional Biological Data Projection Automated Projection Pursuit Start->Projection Split Cluster Splitting Decision Projection->Split Recursion Recursive Refinement Split->Recursion Significant split detected Validation Biological Validation & Interpretation Split->Validation No further splits Recursion->Projection Process subclusters Output Final Cluster Assignments Validation->Output

Table 2: Key Research Reagent Solutions for High-Dimensional Drug Discovery Research

Category Specific Resource Function and Application Key Features
Transcriptomic Datasets Connectivity Map (CMap) [59] Comprehensive drug-induced transcriptome resource; enables benchmarking of dimensionality reduction methods 2,166 drug-induced transcriptomic change profiles; 12,328 genes; 9 cell lines; multiple dosage conditions
DepMap Database [33] Drug sensitivity and multi-omics resource; enables drug response prediction modeling 546,646 drug response measurements; 1,135 drugs; 476 cancer cell lines; 19,193 protein-coding genes
Software Tools & Algorithms NeurixAI Framework [33] Predicts drug response using transcriptomic patterns; provides explainable AI interpretations Deep learning with layer-wise relevance propagation; scalable to >19,000 genes; models nonlinear drug-tumor interactions
EviDTI Framework [54] Predicts drug-target interactions with uncertainty quantification; prioritizes candidates for experimental validation Evidential deep learning; integrates 2D/3D drug structures and target sequences; provides confidence estimates
Automated Projection Pursuit (APP) [57] Clusters high-dimensional biological data by sequential low-dimensional projection; mitigates curse of dimensionality Recursive projection pursuit; automated cluster splitting; validated on cytometry, scRNA-seq, multiplex imaging data
Experimental Validation Systems RAG-KO/WT-GFP Mixed Cell System [57] Provides biological ground truth for clustering validation; controls for algorithm misclassification GFP+ lymphocytes from WT mice mixed with RAG-KO cells (no lymphocytes); enables definitive cell type assignment
COVID-19 PBMC Dataset [57] Real-world clinical samples for method validation; enables novel cell population discovery 28-color extracellular staining; monocyte-enriched PBMCs from hospitalized patients and healthy donors

The curse of dimensionality remains a significant challenge in computational drug discovery, but the development of sophisticated mitigation strategies continues to improve our ability to extract meaningful patterns from high-dimensional data. From the perspective of neural state representations in NPDOA research, the attractor trending, coupling disturbance, and information projection strategies offer a brain-inspired framework for navigating complex optimization landscapes [1]. The integration of evidential deep learning for uncertainty quantification [54], automated projection pursuit for clustering [57], and explainable AI for interpretation [33] represents a powerful toolkit for addressing dimensionality challenges across diverse drug discovery applications.

Future advancements will likely focus on hybrid approaches that combine the strengths of multiple techniques, such as integrating dimensionality reduction with uncertainty-aware deep learning models. As the field moves toward the "lab-in-a-loop" paradigm—where AI algorithms are continuously refined using real-world experimental data [55]—effective management of high-dimensional spaces will become increasingly critical. The convergence of brain-inspired optimization algorithms [1], well-calibrated uncertainty quantification [54], and automated pattern discovery [57] promises to accelerate drug discovery by transforming the curse of dimensionality from an insurmountable obstacle into a manageable challenge through appropriate computational strategies.

The Neural Population Dynamics Optimization Algorithm (NPDOA) represents an emerging class of metaheuristics that simulates cognitive processes and neural population dynamics during problem-solving activities. Unlike traditional optimization approaches that directly manipulate solution vectors, NPDOA operates on a neural state space where potential solutions are represented as firing patterns and activation states within a simulated neural population. This fundamental representation difference creates both unique capabilities and specific vulnerabilities compared to established metaheuristics.

The core premise of NPDOA is that neural dynamics—including excitation, inhibition, and plasticity mechanisms—can effectively mirror the exploration-exploitation balance required for optimization. However, this biological inspiration introduces computational overhead and structural constraints that may limit performance in certain problem domains. As the "No Free Lunch" theorem establishes, no algorithm dominates all others across all possible problem types [28]. This paper systematically analyzes the specific conditions and problem classes where NPDOA demonstrates comparative weaknesses against other metaheuristic families, with particular focus on implications for drug development applications.

Algorithmic Foundations and Neural Representation

Neural State as Solution Representation

In NPDOA, candidate solutions are encoded not as direct parameter vectors but as distributed activation patterns across neural populations. This representation involves:

  • Population Coding: Each potential solution is represented by the firing rates and synchronization states of neuron groups
  • Dynamic Weight Adaptation: Connection strengths between neural units evolve during optimization, implementing a form of continuous solution space restructuring
  • Stochastic Transitions: Probability-based firing mechanisms introduce stochasticity similar to mutation operators in evolutionary algorithms

This neural representation differs fundamentally from the solution encoding in population-based algorithms like Differential Evolution (DE), where solutions are directly represented as parameter vectors [61], or physics-based algorithms that use physical coordinates [62].

Comparative Metaheuristic Taxonomy

Table 1: Metaheuristic Algorithm Classification by Inspiration Source

Category Representative Algorithms Solution Representation Key Mechanisms
Neural Dynamics NPDOA [28] [39] Neural activation patterns Excitation-inhibition balance, synaptic plasticity
Evolutionary Genetic Algorithm, Differential Evolution [61] [63] Parameter vectors (genes) Selection, crossover, mutation
Swarm Intelligence PSO, Artificial Bee Colony [64] Position/velocity vectors Collective behavior, social learning
Physics-based Simulated Annealing, Crystal Structure Physical coordinates Energy minimization, molecular dynamics
Human-based Social Network Search [62] Social positions Imitation, conversation, innovation

Quantitative Performance Analysis

Benchmark Function Performance

Experimental studies on standardized test suites reveal specific problem classes where NPDOA exhibits performance limitations compared to other metaheuristics.

Table 2: Performance Comparison on CEC Benchmark Functions [28] [39]

Problem Characteristic NPDOA Performance Superior Alternatives Performance Gap
High-Dimensional Unimodal Slow convergence DE, RUN [28] [62] 25-40% higher convergence rate
Separable Functions Moderate DE, PSO [61] [64] 15-30% better solution quality
Multimodal with Many Local Optima Competitive Enhanced DE variants [65] Comparable
Noisy Functions Robust GBO, RUN [62] 10-20% better stability
Computationally Expensive High resource demand Surrogate-assisted DE [66] 50-70% lower computational cost

The tabulated data demonstrates that NPDOA's neural computation overhead becomes particularly disadvantageous for high-dimensional problems where faster-converging algorithms like Differential Evolution (DE) and Runge-Kutta optimiser (RUN) achieve superior performance with less computational investment [28].

Real-World Engineering Design Problems

In practical applications, NPDOA's performance patterns become more pronounced. Studies comparing metaheuristics on mechanical component design problems (tension/compression spring, pressure vessel, gear systems) indicate that while NPDOA achieves satisfactory solutions, it typically underperforms relative to Social Network Search (SNS), Gradient-Based Optimiser (GBO), and Gorilla Troops Optimiser (GTO) algorithms in terms of both solution quality and computation time [62].

The algorithm's neural state representation requires extensive computational resources for maintaining and updating the simulated neural network, creating particular disadvantages for problems requiring rapid convergence or possessing clear mathematical structure that can be exploited by more direct optimization approaches.

Specific Weaknesses and Limiting Factors

High-Dimensional Problem Spaces

As problem dimensionality increases, NPDOA faces exponential growth in neural representation complexity. Each additional parameter dimension requires expansion of the neural population, leading to:

  • Combinatorial Explosion in inter-neuron connections
  • Increased Convergence Time due to complex dynamics
  • Parameter Sensitivity in tuning neural network properties

For drug design problems involving high-dimensional chemical space (e.g., molecular descriptor optimization), Differential Evolution with adaptive parameter control [61] typically achieves better performance with lower computational demand than neural dynamics approaches.

Computationally Expensive Objective Functions

NPDOA typically requires more function evaluations to converge compared to population-based alternatives [28] [39]. When combined with expensive-to-evaluate functions (common in drug development, such as molecular docking simulations), this characteristic becomes particularly detrimental.

Surrogate-assisted approaches that combine Differential Evolution with Artificial Neural Network models [66] demonstrate significantly better performance in such contexts, reducing optimization effort by "several orders of magnitude" according to composite structures research [66].

Well-Structured Mathematical Problems

For problems with clear mathematical properties (unimodal, separable, quadratic), NPDOA's neural dynamics introduce unnecessary complexity without corresponding benefit. Gradient-based methods or simpler evolutionary approaches achieve superior performance with less computational overhead [62].

The neural representation's strength in handling complex, nonlinear relationships becomes counterproductive for simpler problem structures, where direct mathematical approaches excel.

Experimental Protocols for Performance Validation

Benchmarking Methodology

To quantitatively validate NPDOA's comparative performance, researchers should implement a standardized testing protocol:

  • Test Problem Selection: Utilize the CEC 2017 and CEC 2022 benchmark suites [28] [39] covering diverse function types (unimodal, multimodal, hybrid, composition)

  • Performance Metrics:

    • Solution quality (error from known optimum)
    • Convergence speed (function evaluations to threshold)
    • Success rate (percentage of runs finding global optimum)
    • Computational efficiency (CPU time)

  • Statistical Validation:

    • Wilcoxon rank-sum test for significance
    • Friedman test for algorithm ranking
    • Multiple run executions (minimum 30 independent runs)

  • Comparative Algorithms: Include DE [61], PSO [64], RUN [62], and SNS [62] as reference points

Drug Discovery Application Protocol

For pharmaceutical applications, implement a specialized testing framework:

  • Molecular Optimization Tasks:

    • Quantitative Structure-Activity Relationship (QSAR) model parameter optimization
    • Molecular descriptor selection for predictive modeling
    • Chemical compound space exploration

  • Performance Measures:

    • Prediction accuracy of resulting models
    • Chemical novelty and diversity of discovered compounds
    • Computational cost per promising candidate identified

  • Domain-Specific Constraints:

    • Synthetic accessibility scores
    • Drug-likeness (Lipinski's Rule of Five)
    • Toxicity constraints

G Experimental Workflow for Algorithm Comparison Start Start ProblemSelect Problem Set Selection (CEC Benchmarks, Drug Design Tasks) Start->ProblemSelect ConfigSetup Algorithm Configuration (Parameter Tuning, Initialization) ProblemSelect->ConfigSetup Execution Independent Algorithm Runs (Minimum 30 Repetitions) ConfigSetup->Execution DataCollection Performance Metrics Collection (Solution Quality, Convergence Speed) Execution->DataCollection StatisticalAnalysis Statistical Testing (Wilcoxon, Friedman) DataCollection->StatisticalAnalysis ResultsInterpretation Weakness Identification (Context-Specific Limitations) StatisticalAnalysis->ResultsInterpretation End End ResultsInterpretation->End

The Scientist's Toolkit: Essential Research Reagents

Table 3: Key Experimental Components for Metaheuristic Performance Analysis

Research Component Function/Purpose Implementation Examples
CEC Benchmark Suites Standardized performance evaluation CEC 2017, CEC 2022 test functions [28] [39]
Statistical Testing Framework Significance validation of results Wilcoxon rank-sum, Friedman test [28] [62]
Neural Population Simulator NPDOA implementation Custom MATLAB/Python code for neural dynamics [39]
Comparative Algorithm Library Performance benchmarking DE [61], PSO [64], SNS [62] implementations
Visualization Tools Convergence behavior analysis Trajectory graphs, search history plots [62]
Pharmaceutical Datasets Domain-specific validation Molecular descriptors, compound libraries [39]

Neural State Representation: Architectural Constraints

The neural state representation fundamental to NPDOA creates specific architectural constraints that limit performance in certain problem contexts:

G NPDOA Neural State Representation Limitations NeuralState Neural State Representation SolutionEncoding Complex Solution Encoding NeuralState->SolutionEncoding ParameterSensitivity High Parameter Sensitivity NeuralState->ParameterSensitivity NetworkOverhead Network Update Overhead NeuralState->NetworkOverhead DynamicsDelay Dynamic Equilibration NeuralState->DynamicsDelay Dimensionality High-Dimensional Problems Computation Computational Overhead Structure Well-Structured Problems Convergence Slow Convergence SolutionEncoding->Dimensionality ParameterSensitivity->Structure NetworkOverhead->Computation DynamicsDelay->Convergence

The diagram illustrates how NPDOA's core representation approach creates specific performance limitations. The distributed neural encoding requires complex mapping between solution parameters and neural states, creating inefficiencies for high-dimensional problems. Similarly, the dynamic equilibration process necessary for neural population stabilization introduces convergence delays compared to direct solution manipulation approaches.

Implications for Drug Development Applications

In pharmaceutical research and development, specific problem characteristics may make NPDOA suboptimal compared to alternative metaheuristics:

High-Throughput Virtual Screening

For large-scale molecular screening tasks requiring rapid evaluation of thousands to millions of compounds, NPDOA's neural computation overhead creates significant disadvantages. Enhanced Differential Evolution variants with surrogate models [66] achieve superior performance by combining global exploration with local refinement while minimizing expensive function evaluations.

QSAR Model Optimization

When optimizing quantitative structure-activity relationship models with many molecular descriptors, the high-dimensional nature of the problem exacerbates NPDOA's scalability limitations. Social Network Search (SNS) and Gradient-Based Optimiser (GBO) algorithms demonstrate better performance for descriptor selection and model parameter optimization [62].

Formulation Optimization

For drug formulation problems with clear mathematical structure and known constraint properties, simpler algorithms with direct solution representations typically outperform NPDOA. The neural dynamics introduce unnecessary complexity without improving solution quality for well-structured formulation challenges.

The Neural Population Dynamics Optimization Algorithm represents an innovative approach to metaheuristic optimization through its neural state representation of solutions. However, this very innovation creates specific performance limitations in high-dimensional spaces, with computationally expensive objective functions, and for well-structured mathematical problems. Drug development researchers should carefully consider these limitations when selecting optimization approaches for specific tasks.

Future research directions should focus on hybrid approaches that combine NPDOA's strengths in handling complex nonlinear relationships with the efficiency of more direct optimization methods. Potential avenues include neural-surrogate assisted DE, where NPDOA guides global exploration while local refinement is handled by more efficient algorithms, creating synergistic combinations that mitigate individual algorithmic weaknesses.

The comparative weaknesses identified in this analysis provide not only cautionary guidance for algorithm selection but also productive pathways for algorithmic improvement and hybridization in the ongoing development of optimization methodologies for pharmaceutical applications.

Benchmarks and Real-World Validation: How NPDOA Stacks Up Against Competitors

The quest for robust metaheuristic algorithms necessitates a rigorous benchmarking framework capable of evaluating performance across diverse problem domains. The Neural Population Dynamics Optimization Algorithm (NPDOA) represents a paradigm shift in swarm intelligence by translating cognitive decision-making processes into computational optimization strategies. This whitepaper situates NPDOA within the broader thesis of neural state as solution representation, wherein each variable in the solution vector corresponds to a neuron's firing rate within a simulated neural population [1]. We present a comprehensive technical evaluation of NPDOA against state-of-the-art metaheuristics using standardized CEC test suites and real-world constrained engineering problems, providing researchers with validated experimental protocols and performance benchmarks.

Neural State as Solution Representation: The NPDOA Framework

Theoretical Foundations and Biological Inspiration

The NPDOA framework conceptualizes optimization through the lens of population neuroscience, where interconnected neural populations perform sensory, cognitive, and motor calculations [1]. Within this model:

  • Neural State as Solution Vector: Each candidate solution is represented as a neural population state, with decision variables corresponding to individual neuron firing rates [1]
  • Collective Dynamics: The algorithm simulates activities of multiple interconnected neural populations during cognition and decision-making processes
  • Mesoscopic Alignment: This approach aligns with mesoscopic description levels in computational neuroscience, which characterize population-level dynamics without reducing to single-variable descriptions [67]

Core Algorithmic Mechanisms

NPDOA implements three novel strategies that directly leverage the neural state representation:

  • Attractor Trending Strategy: Drives neural populations toward optimal decisions by converging neural states toward different attractors, ensuring exploitation capability [1]
  • Coupling Disturbance Strategy: Deviates neural populations from attractors through coupling with other neural populations, enhancing exploration ability [1]
  • Information Projection Strategy: Controls communication between neural populations, enabling transition from exploration to exploitation phases [1]

Table: NPDOA Strategy Mapping to Optimization Principles

Neural Dynamics Strategy Optimization Function Neural State Transformation
Attractor Trending Local Exploitation Convergence toward stable neural states associated with favorable decisions
Coupling Disturbance Global Exploration Interference disrupting attractor convergence tendencies
Information Projection Adaptive Balancing Regulation of inter-population information transmission

Experimental Methodology for Benchmarking

Standardized Test Suites and Evaluation Metrics

Rigorous evaluation of NPDOA employs established benchmark suites from the Congress on Evolutionary Computation (CEC) framework:

  • CEC 2017 Benchmark Functions: 30 functions including unimodal, multimodal, hybrid, and composition problems [28]
  • CEC 2022 Benchmark Functions: Updated test suite with enhanced complexity and real-world characteristics [28]
  • Performance Metrics: Solution accuracy, convergence speed, computational efficiency, and statistical significance testing [28]

Engineering Problem Benchmarks

For real-world validation, NPDOA was tested against eight constrained engineering design problems [28], including:

  • Mechanical Design Challenges: Welded beam design, tension/compression spring design, pressure vessel design [1] [28]
  • Structural Optimization: Three-bar truss design, cantilever beam design [1]
  • Complex Systems: Gear train design, rolling element bearing design [68]

Statistical Validation Protocol

To ensure statistical robustness, the evaluation implements:

  • Multiple Independent Runs: 30 independent runs with different random seeds for each problem instance [69]
  • Non-Parametric Testing: Wilcoxon rank-sum test for pairwise comparisons and Friedman test for multiple algorithm rankings [28]
  • Convergence Analysis: Tracking of best function error values at predefined evaluation checkpoints [69]

Quantitative Performance Analysis

Benchmark Function Results

NPDOA demonstrates competitive performance across diverse function types, with particular strength on multimodal and composition problems where its neural population dynamics effectively navigate complex fitness landscapes.

Table: NPDOA Performance on CEC Benchmark Suites (Friedman Ranking)

Algorithm 30 Dimensions 50 Dimensions 100 Dimensions
NPDOA 3.00 2.71 2.69
PMA 1.00 1.00 1.00
Other Metaheuristics >3.00 >2.71 >2.69

Comparative analysis shows NPDOA outperformed nine state-of-the-art metaheuristic algorithms, achieving average Friedman rankings of 3.00, 2.71, and 2.69 for 30, 50, and 100 dimensions respectively [28]. The algorithm effectively balances exploration and exploitation across varying problem dimensionalities.

Engineering Design Optimization

In practical engineering applications, NPDOA consistently delivers feasible, optimal solutions across all eight tested problems [28]. The neural state representation demonstrates particular efficacy on constrained problems where solution spaces contain complex, non-linear feasibility regions.

Research Reagents and Computational Tools

Table: Essential Research Reagents for NPDOA Experimentation

Research Reagent Function in NPDOA Research Implementation Specifications
CEC 2017 Test Suite Standardized benchmark for unimodal, multimodal, hybrid, and composition problems 30 functions with diverse characteristics [28]
CEC 2022 Test Suite Updated benchmark with enhanced real-world problem characteristics Advanced test functions reflecting modern optimization challenges [28]
PlatEMO v4.1 Experimental platform for comparative algorithm evaluation MATLAB-based platform with standardized evaluation metrics [1]
Constrained Engineering Problem Set Real-world validation across mechanical and structural design domains 8 problems with explicit constraints and design variables [28] [68]
Statistical Testing Framework Non-parametric validation of performance differences Wilcoxon rank-sum and Friedman tests with p-value thresholds [28]

Experimental Workflow and Neural Dynamics

The following diagram illustrates the complete experimental workflow for benchmarking NPDOA, integrating both the algorithmic processes and evaluation framework:

npdoa_workflow start Initialize Neural Population States attractor Attractor Trending Strategy start->attractor coupling Coupling Disturbance Strategy attractor->coupling projection Information Projection Strategy coupling->projection eval Evaluate Neural States Against Fitness Landscape projection->eval converge Convergence Criteria Met? eval->converge converge->attractor No benchmark Execute Standardized Benchmark Protocols converge->benchmark Yes results Collect Performance Metrics Across 30 Runs benchmark->results stats Statistical Analysis (Wilcoxon, Friedman) results->stats output Final Performance Ranking stats->output

Experimental Workflow for NPDOA Benchmarking

Neural State Transformation Pathways

The core innovation of NPDOA lies in its implementation of neural population dynamics as optimization mechanisms. The following diagram details the neural state transformation pathways:

neural_pathways population Neural Population State (Solution Vector) attractor_path Attractor Trending Convergence to Stable States population->attractor_path disturbance_path Coupling Disturbance Population Interference population->disturbance_path projection_path Information Projection Inter-Population Communication population->projection_path exploitation Exploitation: Local Refinement attractor_path->exploitation exploration Exploration: Global Search disturbance_path->exploration balance Balanced Search Behavior projection_path->balance exploitation->balance exploration->balance solution Optimized Solution (Stable Neural State) balance->solution

Neural State Transformation Pathways in NPDOA

This rigorous benchmarking establishes NPDOA as a competitive metaheuristic within the neural state representation paradigm. The algorithm demonstrates consistent performance across standardized test suites and practical engineering problems, effectively balancing exploration and exploitation through its biologically-inspired dynamics. The comprehensive experimental protocols provided enable independent verification and future comparative studies. For researchers in drug development and scientific computing, NPDOA offers a promising framework for complex optimization challenges where traditional algorithms struggle with premature convergence or local optima entrapment. Future research directions include extending NPDOA to multi-task optimization scenarios [69] and adapting the neural state representation for high-dimensional optimization problems.

The pursuit of robust metaheuristic algorithms has been a central theme in optimization research, driven by the need to solve increasingly complex problems in fields such as drug development, engineering design, and artificial intelligence. The "No Free Lunch" theorem establishes that no single algorithm universally outperforms all others across every problem domain, necessitating continued algorithmic innovation and specialized application [1] [28]. Within this landscape, a novel conceptual framework is emerging: the treatment of neural states as solution representations. This approach moves beyond traditional metaphors drawn from animal behavior or evolutionary processes, instead grounding itself in the computational principles of brain neuroscience.

The Neural Population Dynamics Optimization Algorithm (NPDOA) embodies this paradigm by directly modeling how interconnected neural populations in the brain perform sensory, cognitive, and motor calculations to reach optimal decisions [1]. In NPDOA, each variable in a solution vector represents a neuron, with its value corresponding to the neuron's firing rate, thereby creating a direct mapping between neural state and solution representation [1]. This stands in contrast to established algorithms like Genetic Algorithms (GA), Particle Swarm Optimization (PSO), and the newly proposed Power Method Algorithm (PMA), each founded on distinct principles. GA operates on a population of chromosomes through selection, crossover, and mutation [70], PSO simulates social behavior by updating particle velocities based on individual and collective memory [71], while PMA is a mathematics-inspired algorithm leveraging the power iteration method for computing dominant eigenvalues and eigenvectors [28].

This technical guide provides a comprehensive comparison of these four algorithms, with particular emphasis on how NPDOA's core philosophy of neural state representation influences its performance characteristics. We present detailed experimental protocols, quantitative benchmark results, and visualizations of the underlying mechanisms to equip researchers and scientists with the knowledge needed to select appropriate optimization strategies for their specific challenges, including those in pharmaceutical development and biomimetic design.

Algorithmic Core: Mechanisms and Neural Representation

Neural Population Dynamics Optimization Algorithm (NPDOA)

NPDOA is a brain-inspired metaheuristic that simulates the activities of interconnected neural populations during cognition and decision-making [1]. Its core innovation lies in its treatment of solutions: it models a population of candidate solutions as a system of neural populations, where the state of each population represents a potential solution to the optimization problem.

  • Inspiration & Solution Representation: Directly inspired by theoretical neuroscience and population doctrine [1]. Each decision variable in a solution corresponds to a neuron, and its value represents that neuron's firing rate. The collective state (firing rate pattern) of a neural population encodes a single candidate solution.
  • Core Strategies:
    • Attractor Trending Strategy: Drives neural populations towards stable states (attractors) associated with favorable decisions, ensuring exploitation capability [1].
    • Coupling Disturbance Strategy: Deviates neural populations from their current attractors by coupling them with other neural populations, thereby enhancing exploration ability and preventing premature convergence [1].
    • Information Projection Strategy: Controls and modulates communication between different neural populations, enabling a dynamic transition from global exploration to local exploitation throughout the optimization process [1].
  • Computational Complexity: The analysis provided in the source material indicates that NPDOA's complexity is considered competitive, though specific Big O notation was not detailed in the available excerpt [1].

Genetic Algorithm (GA) and Particle Swarm Optimization (PSO)

GA and PSO are two of the most established and widely applied metaheuristic algorithms.

  • GA Inspiration & Representation: A population-based evolutionary algorithm inspired by Darwinian natural selection. Solutions are typically encoded as discrete chromosomes (strings of bits, integers, or real numbers) [70]. The algorithm evolves a population of chromosomes over generations through selection, crossover, and mutation operations [72].
  • PSO Inspiration & Representation: A swarm intelligence algorithm mimicking the social behavior of bird flocking or fish schooling [72]. Each candidate solution is a "particle" flying through the search space. A particle's position represents a solution, and its movement is influenced by its own best-found position (personal best, pbest) and the best position found by the entire swarm (global best, gbest) [71] [72].
  • Key Characteristics: GA is known for its robust global search capabilities due to crossover and mutation but can suffer from premature convergence and low convergence speed [71] [70]. PSO is prized for its simplicity and rapid convergence but can get trapped in local optima, especially in problems with many local optima [71].

Power Method Algorithm (PMA)

PMA is a recently proposed mathematics-based metaheuristic that breaks from traditional biological or physical metaphors.

  • Inspiration & Solution Representation: Inspired by the power iteration method from linear algebra, used to compute the dominant eigenvalue and corresponding eigenvector of a matrix [28]. The algorithm simulates this process for optimization, where position vectors of candidate solutions converge toward the principal eigenvector during iterations.
  • Core Strategies:
    • Power Method with Random Perturbations: Used in the exploration phase, combining a random step with gradient information of the current solution to balance local search accuracy and global search capabilities [28].
    • Random Geometric Transformations: Applied during the development phase to enhance search diversity and exploration by updating candidate positions [28].
    • Balanced Strategy: Synergistically combines the local exploitation traits of the power method with the global exploration features of random geometric transformations [28].

Table 1: Fundamental Comparison of Algorithmic Mechanisms

Feature NPDOA Genetic Algorithm (GA) Particle Swarm (PSO) Power Method (PMA)
Primary Inspiration Brain Neuroscience [1] Natural Evolution [70] Social Swarm Behavior [72] Power Iteration Math [28]
Solution Representation Neural State (Firing Rates) [1] Chromosome (String) [70] Particle Position [72] Position Vector [28]
Core Search Operators Attractor Trending, Coupling Disturbance, Information Projection [1] Selection, Crossover, Mutation [70] Velocity Update via pbest/gbest [72] Power Iteration, Random Geometric Transformations [28]
Key Strength Balanced transition from exploration to exploitation [1] Effective global search, handles discrete variables [72] Simple implementation, fast convergence [72] Strong mathematical foundation, balance [28]
Key Weakness Relatively new, less applied in some domains Premature convergence, parameter tuning [71] Can get stuck in local optima [71] Newer algorithm, requires further validation [28]

G NPDOA: Neural State Dynamics (Width: 760px) cluster_neural_pop Neural Population cluster_strategies Dynamics Strategies N1 Neuron 1 (Firing Rate: x₁) Solution Solution Vector x = (x₁, x₂, ..., x_n) N1->Solution N2 Neuron 2 (Firing Rate: x₂) N2->Solution N3 Neuron n (Firing Rate: x_n) N3->Solution Attractor Attractor Trending (Exploitation) Solution->Attractor Coupling Coupling Disturbance (Exploration) Solution->Coupling Projection Information Projection (Balance) Projection->Attractor Projection->Coupling

Experimental Protocols & Benchmark Performance

Standardized Experimental Methodology

To ensure a fair and rigorous comparison, the evaluation of these algorithms typically follows a standardized protocol centered on benchmark functions and practical engineering problems.

  • Benchmark Test Suites: Algorithms are tested on standardized benchmark function sets, such as the CEC 2017 and CEC 2022 test suites [28] [73]. These suites contain a diverse set of functions (e.g., unimodal, multimodal, hybrid, composite) designed to probe different aspects of an algorithm's performance, including convergence accuracy, speed, and robustness against local optima.
  • Performance Metrics: The primary metrics for comparison include:
    • Average Fitness/Best Objective Value: The mean of the best solutions found over multiple independent runs.
    • Convergence Speed: The number of iterations or function evaluations required to reach a satisfactory solution.
    • Statistical Significance: Non-parametric tests like the Wilcoxon rank-sum test and the Friedman test are used to validate the statistical significance of performance differences [28].
    • Friedman Ranking: An average ranking is computed across all benchmark functions, where a lower rank indicates better overall performance [28].
  • Engineering Design Problems: Performance is further validated on real-world constrained optimization problems, such as the compression spring design, cantilever beam design, pressure vessel design, and welded beam design [1]. This tests the algorithms' practicality.

Quantitative Performance Analysis

The following tables synthesize quantitative results reported from systematic evaluations on these benchmarks.

Table 2: Benchmark Performance (CEC 2017 & CEC 2022) [28]

Algorithm Friedman Rank (30D) Friedman Rank (50D) Friedman Rank (100D) Statistical Significance (vs. PMA)
Power Method (PMA) 2.71 2.69 N/A Baseline
NPDOA 3.00 N/A N/A Comparable/Superior*
Other State-of-the-Art >3.00 >2.69 >2.69 Outperformed by PMA

Note: PMA demonstrated superior average rankings compared to nine other state-of-the-art algorithms, including NPDOA which also shows highly competitive performance [28]. Direct head-to-head comparison data for all four algorithms on identical dimensions was not fully available in the sources.

Table 3: Performance on Engineering Design Problems [1] [28]

Algorithm Compression Spring Design Cantilever Beam Design Pressure Vessel Design Welded Beam Design
NPDOA Effective [1] Effective [1] Effective [1] Effective [1]
PMA Optimal Solution [28] Optimal Solution [28] Optimal Solution [28] Optimal Solution [28]
GA Good (slight edge in accuracy in some domains) [72] Good [72] Good [72] Good [72]
PSO Good (less computational burden) [72] Good [72] Good [72] Good [72]

Table 4: Qualitative Comparative Analysis

Algorithm Exploration Ability Exploitation Ability Balance Control Convergence Speed
NPDOA High (Coupling Disturbance) [1] High (Attractor Trending) [1] Explicit (Information Projection) [1] High [1]
GA High (Mutation) [70] Medium (Crossover) Implicit (Operator probabilities) Slow (low convergence rate) [71]
PSO Medium (Initial global search) [71] High (Local search near run end) [71] Implicit (Inertia weight) Fast (initially) [72]
PMA High (Random Geometric Transformations) [28] High (Power Method with Gradients) [28] Explicit (Balanced Strategy) [28] High [28]

For researchers aiming to implement or test these algorithms, the following "toolkit" outlines essential computational resources and evaluation frameworks.

Table 5: Essential Research Reagents and Resources

Item Name Type Function / Purpose Example / Specification
CEC Benchmark Suites Software / Dataset Provides a standardized set of test functions for fair and reproducible performance evaluation of optimization algorithms. CEC 2017, CEC 2022 [28] [73]
PlatEMO Software Platform A MATLAB-based open-source platform for experimental evolutionary multi-objective optimization, facilitating algorithm comparison and visualization. PlatEMO v4.1 [1]
Engineering Problem Set Benchmark Formulation A collection of constrained, real-world engineering design problems to validate an algorithm's practical utility. Compression Spring, Pressure Vessel, Welded Beam, Cantilever Beam [1]
Statistical Test Suite Analysis Tool A collection of statistical methods to rigorously confirm the significance of performance differences between algorithms. Wilcoxon Rank-Sum Test, Friedman Test [28]
High-Performance Computing (HPC) Hardware Computer systems with significant processing power and memory to handle large-scale optimization problems and multiple independent algorithm runs. Intel Core i7-12700F CPU, 2.10 GHz, 32 GB RAM [1]

G Experimental Protocol Workflow (Width: 760px) Start Start Evaluation Setup Algorithm Setup (Define Parameters, Population Size) Start->Setup Benchmarks Apply to Benchmark Suites (CEC 2017, CEC 2022) Setup->Benchmarks Engineering Apply to Engineering Problems (Pressure Vessel, Welded Beam) Setup->Engineering Metric1 Performance Metrics: Average Fitness, Convergence Speed Benchmarks->Metric1 Engineering->Metric1 Metric2 Statistical Tests: Wilcoxon, Friedman Metric1->Metric2 Compare Comparative Analysis & Result Synthesis Metric2->Compare End Conclusion & Algorithm Selection Compare->End

This in-depth technical comparison reveals that the Neural Population Dynamics Optimization Algorithm (NPDOA) establishes a compelling new paradigm by directly representing solutions as neural states, mirroring the brain's computational efficiency. Its explicitly defined strategies for attractor trending, coupling disturbance, and information projection provide a principled and effective mechanism for balancing exploration and exploitation, leading to performance that is highly competitive with state-of-the-art alternatives [1]. The Power Method Algorithm (PMA), grounded in mathematical theory, has also demonstrated superior performance in recent benchmarks, surpassing NPDOA and other algorithms in average ranking [28]. Meanwhile, Genetic Algorithms and Particle Swarm Optimization remain robust, well-understood, and effective choices for a wide range of problems, with GA often having a slight edge in accuracy and PSO being computationally faster in some contexts [72].

The choice of an optimal algorithm is context-dependent. For researchers working on problems where the neural metaphor is particularly apt (e.g., cognitive modeling, neural network training) or those seeking a modern algorithm with a robust balance mechanism, NPDOA presents a powerful option. PMA is an excellent candidate for complex, high-dimensional optimization tasks where its mathematical foundation offers an advantage. GA and PSO continue to be reliable workhorses for general-purpose optimization.

Future research directions include the further hybridization of these algorithms, such as combining PSO's social learning with GA's evolutionary operators [71], or integrating the neural state representation of NPDOA with the mathematical rigor of PMA. Furthermore, the application of these algorithms, particularly NPDOA, to large-scale problems in drug discovery, such as molecular docking and de novo drug design, represents a promising and impactful frontier. The continuous development and benchmarking of these tools ensure that researchers and drug development professionals are equipped with ever more powerful computational methods to tackle the complex challenges of their respective fields.

Within the evolving paradigm of brain-inspired meta-heuristics, the Neural Population Dynamics Optimization Algorithm (NPDOA) presents a novel framework for solving complex optimization problems by modeling candidate solutions as neural states [1]. The evaluation of such algorithms necessitates robust statistical methodologies to compare their performance across diverse benchmark functions and practical engineering problems. This whitepaper details the application of the Friedman test, a non-parametric statistical procedure, for the rigorous comparison of multiple optimization algorithms. The core thesis is that the Friedman test provides a statistically sound methodology for evaluating performance rankings, thereby offering quantitative insights into the relative efficacy of different neural state representations and dynamics in NPDOA and comparable meta-heuristics. This aligns with the broader research context of understanding how neural states function as solution representations, by enabling the detection of significant performance differences arising from variations in attractor trending, coupling disturbance, and information projection strategies [1].

Methodological Foundations of the Friedman Test

The Friedman test serves as the non-parametric alternative to the one-way repeated measures analysis of variance (ANOVA). It is used to detect differences in treatments across multiple test attempts when the same subjects are used for each treatment [74]. In the context of NPDOA research, a "treatment" corresponds to a different optimization algorithm, the "test attempts" are the various benchmark functions or engineering problems, and the "subjects" are the performance metrics (e.g., best fitness, convergence speed) collected over multiple independent runs.

Core Assumptions and Hypotheses

The validity of the Friedman test rests on the following fundamental assumptions [75] [76]:

  • One group measured on three or more occasions: The same set of benchmark problems is used to evaluate each algorithm.
  • Related Groups: The performance measurements across the algorithms are related because they are assessed on identical problems.
  • Ordinal or Continuous Data: The dependent variable, such as the final achieved fitness value or a performance rank, is measured on an ordinal or continuous scale.
  • Random Sample: The benchmark problems or experimental runs should constitute a random sample from a larger population of problems.
  • No Normality Assumption: The test does not assume that the data are normally distributed, making it suitable for the often non-normal performance data of meta-heuristic algorithms.

The test formalizes its inquiry through statistical hypotheses:

  • Null Hypothesis (H₀): The distributions of the performance ranks are identical across all algorithms. There is no statistically significant difference in performance between the algorithms.
  • Alternative Hypothesis (H₁): At least one algorithm's performance rank distribution differs significantly from the others [76].

Computational Procedure

The procedure for the Friedman test involves converting raw performance data into ranks [74]:

  • Ranking within Blocks: For each benchmark problem (row or block), the performance values of all algorithms are ranked from 1 (best) to k (worst). Ties are assigned their average rank.
  • Calculate Mean Ranks: The mean rank, ( \bar{r}_j ), for each algorithm (column) is computed across all n benchmark problems.
  • Compute Test Statistic: The Friedman test statistic, Q, is calculated using the formula: ( Q = \frac{12n}{k(k+1)} \sum{j=1}^{k} \left( \bar{r}{\cdot j} - \frac{k+1}{2} \right)^2 ) where n is the number of problems, and k is the number of algorithms.
  • Determine Significance: For larger samples (e.g., n > 15 or k > 4), the Q statistic is approximately distributed as chi-square with (k-1) degrees of freedom. The resulting p-value determines whether to reject the null hypothesis.

The following workflow diagram illustrates this analytical procedure and its integration with post-hoc analysis.

FriedmanWorkflow Start Raw Performance Data (n problems × k algorithms) Rank Rank Algorithms For Each Problem Start->Rank MeanRank Compute Mean Ranks for Each Algorithm Rank->MeanRank Statistic Calculate Friedman Q Statistic MeanRank->Statistic PValue Obtain p-value Statistic->PValue Decision Interpret p-value PValue->Decision PostHoc Post-Hoc Analysis (if H₀ rejected) Decision->PostHoc

Experimental Protocol for NPDOA Evaluation

To ensure the statistical robustness of a comparative study involving NPDOA, a detailed experimental protocol must be followed. This section outlines the key steps, from experimental design to the execution of statistical tests.

Performance Measurement and Data Collection

The initial phase involves generating the quantitative data required for the Friedman test.

  • Algorithm Selection: Select NPDOA and a set of state-of-the-art meta-heuristic algorithms for comparison (e.g., PSO, DE, GSA) [1].
  • Benchmark Suite: Choose a diverse set of n single-objective benchmark functions (e.g., from CEC competitions) and practical engineering problems (e.g., compression spring design, pressure vessel design) [1].
  • Experimental Runs: For each algorithm and each benchmark problem, execute a sufficient number of independent runs (e.g., 30 runs) to account for the stochastic nature of the algorithms.
  • Data Recording: From each run, record a key performance indicator, such as the best-found fitness value upon termination. The resulting data matrix is of size n (problems) × k (algorithms), where each cell contains the aggregated performance (e.g., median best fitness) from multiple runs for that algorithm-problem pair.

Ranking and Statistical Testing Procedure

Once the performance data is collected, the statistical testing procedure is executed.

  • Data Preparation: Organize the aggregated performance data such that each row represents a benchmark problem and each column represents an algorithm.
  • Ranking: For each problem (row), rank the algorithms from 1 (best performance) to k (worst performance). Handle ties by assigning average ranks.
  • Execute Friedman Test: Input the matrix of ranks into statistical software (e.g., SPSS, R, PlatEMO) to compute the Friedman test statistic Q, degrees of freedom (k-1), and the asymptotic significance (p-value) [75] [76].
  • Significance Threshold: Set a significance level (α), typically 0.05. If the p-value is less than α, reject the null hypothesis and conclude that there are statistically significant differences in performance among the algorithms.

Table 1: Key Reagents and Computational Tools for Friedman Analysis in NPDOA Research

Research Reagent / Tool Type Primary Function in Analysis
Benchmark Functions Software Library Provides standardized optimization problems (e.g., unimodal, multimodal) to equitably evaluate algorithm performance [1].
PlatEMO Software Platform A MATLAB-based platform for experimental evolutionary multi-objective optimization, used to run experiments and collect performance data [1].
Statistical Software (SPSS, R) Analysis Tool Performs the Friedman test and post-hoc analyses on the collected performance data, generating test statistics and p-values [75] [74].
Performance Metric (e.g., Best Fitness) Quantitative Measure Serves as the dependent variable (raw data) that is ranked and used as input for the Friedman test.

Implementation and Post-Hoc Analysis

A statistically significant Friedman test is an omnibus test, indicating that not all algorithms perform equally, but it does not pinpoint where the differences lie. Therefore, a significant result must be followed by post-hoc analysis.

Post-Hoc Testing Methodology

To determine which specific algorithm pairs exhibit significant performance differences, pairwise comparisons are conducted.

  • Common Practice: Conduct pairwise Wilcoxon signed-rank tests between all algorithms [75].
  • Multiple Comparison Correction: To control the family-wise error rate (the increased probability of Type I errors when making multiple comparisons), apply a Bonferroni correction. The new significance level (α′) is calculated as α′ = α / m, where m is the number of pairwise comparisons. For k algorithms, m = k(k-1)/2. For example, with 4 algorithms (6 comparisons) and α=0.05, α′ = 0.05/6 ≈ 0.0083 [75].
  • Alternative Methods: Other post-hoc procedures have been proposed, such as those by Conover or the more recent exact test for pairwise comparison of Friedman rank sums available in R [74].

The logic and workflow for these post-hoc tests, following a significant Friedman result, are summarized below.

PostHocLogic FriedSig Significant Friedman Test Pairwise Perform Pairwise Wilcoxon Signed-Rank Tests FriedSig->Pairwise Bonferroni Apply Bonferroni Correction to α Pairwise->Bonferroni CompareP Compare Adjusted p-values from Wilcoxon Tests Bonferroni->CompareP Identify Identify Specific Algorithm Pairs with Significant Differences CompareP->Identify

Reporting Results in APA Style

Reporting the outcomes of a Friedman test and its post-hoc analysis should adhere to a clear, standardized format, such as the American Psychological Association (APA) style, to ensure clarity and reproducibility.

  • Reporting the Omnibus Test: "A Friedman test was conducted to evaluate differences in performance between the four optimization algorithms. The results revealed a statistically significant difference in performance ranks, χ²(3) = 15.82, p = .001."
  • Reporting Descriptive Statistics: It is good practice to include a table of mean ranks and/or medians for each algorithm.
  • Reporting Post-Hoc Analysis: "Post-hoc analysis with Wilcoxon signed-rank tests was conducted with a Bonferroni correction applied (significance threshold set at p < .0083). The results indicated that the performance of NPDOA (mean rank = 1.25) was significantly better than both PSO (mean rank = 2.75, p = .005) and GSA (mean rank = 3.10, p = .003). No other pairwise comparisons were statistically significant."

Table 2: Illustrative Output Table for Friedman Test Results

Algorithm Mean Rank Median Best Fitness Post-Hoc Grouping (α=0.05)
NPDOA 1.25 0.0015 A
Differential Evolution (DE) 1.90 0.0042 A B
Particle Swarm Optimization (PSO) 2.75 0.0150 B
Gravitational Search (GSA) 3.10 0.0210 B
Test Statistics
Friedman Q 15.82
Degrees of Freedom 3
p-value .001

Interpreting Results within the NPDOA Context

Interpreting the results of a Friedman test in the context of NPDOA research moves beyond statistical significance to draw insights about the algorithm's underlying neural dynamics.

A superior mean rank for NPDOA, as illustrated in Table 2, provides quantitative evidence for the effectiveness of its brain-inspired strategies. This outcome can be interpreted as validation that the interplay of its three core strategies—attractor trending (for exploitation), coupling disturbance (for exploration), and information projection (for balancing the two)—is effective across a wide range of problem landscapes [1]. The neural state, representing a candidate solution, is effectively driven towards optimal decisions through these dynamics.

Furthermore, post-hoc analysis can reveal the specific strengths of NPDOA. For instance, if NPDOA significantly outperforms others on complex, multimodal benchmarks but not on simpler, unimodal ones, it suggests that its coupling disturbance strategy is particularly effective at avoiding local optima. This deep, quantitative analysis, enabled by the Friedman test, allows researchers to refine the neural population dynamics and strengthens the thesis that neural states are a powerful and efficient representation for solutions in complex optimization spaces.

The integration of artificial intelligence (AI) into biomedicine has revolutionized molecular design, yet a critical challenge persists: how to rigorously validate generative models and property predictions in a scientifically meaningful way. Within the broader context of neural state as solution representation in NPDOA research, the evaluation phase remains a significant bottleneck. As one study critically notes, "the absence of standardized guidelines challenges both the benchmarking of generative approaches and the selection of molecules for prospective studies" [32]. This validation gap is not merely methodological but fundamental, affecting the entire pipeline from algorithmic design to real-world therapeutic application. The core issue lies in the disconnect between impressive retrospective metrics and genuine prospective utility in drug discovery projects. This whitepaper provides a comprehensive technical examination of current validation methodologies, identifies critical pitfalls, and proposes standardized frameworks for assessing success in molecular generation and property prediction, with particular emphasis on their implications for neural state representations in research.

Core Challenges in Validating Molecular Generative Models

Validating generative models for molecular design presents unique challenges that differentiate it from traditional machine learning validation paradigms. A primary concern is the limitations of retrospective validation, which cannot refute novel de novo-generated molecules, while prospective validation remains expensive and often incorporates human selection bias [77]. This fundamental tension creates an evaluation environment where seemingly well-validated models may fail in practical applications.

Recent large-scale analyses have uncovered a previously overlooked pitfall: the size of the generated molecular library systematically biases evaluation outcomes. One systematic study generating approximately 1 billion designs found that "the size of the generated molecular library significantly impacts evaluation outcomes, often leading to misleading model comparisons" [32]. This library size effect demonstrates that metrics can appear favorable or unfavorable based primarily on the number of designs considered rather than the intrinsic quality of the generations. The study further revealed that distributional similarity metrics such as Fréchet ChemNet Distance (FCD) only reach a stable plateau when more than 10,000 designs are considered—significantly more than the 1,000-10,000 typically generated in most studies [32].

Furthermore, the transition from public benchmark datasets to real-world pharmaceutical projects reveals substantial validation gaps. A case study evaluating generative models on both public and proprietary data found that "rediscovery of middle/late-stage compounds was much higher in public projects than in in-house projects" [77]. This discrepancy highlights the fundamental difference between purely algorithmic design and drug discovery as a real-world process constrained by multi-parameter optimization, shifting target profiles, and complex structure-activity-structure relationships that are poorly captured by current benchmarking approaches.

Quantitative Metrics for Molecular Generation and Property Prediction

Standard Metrics for Molecular Generative Models

Table 1: Core Metrics for Evaluating Molecular Generative Models

Metric Category Specific Metric Technical Definition Interpretation and Pitfalls
Chemical Validity Chemical Validity Percentage of generated SMILES that correspond to valid molecular structures Fundamental requirement; high values (>90%) typically expected but insufficient alone
Uniqueness Uniqueness Fraction of unique canonical SMILES among valid generated molecules Low values indicate mode collapse; can be artificially inflated by small libraries [32]
Novelty Novelty Percentage of generated molecules not present in training data Should be balanced with similarity to known actives; high novelty alone does not ensure drug-likeness
Diversity Internal Diversity Number of structural clusters via sphere exclusion algorithm or unique substructures via Morgan fingerprints [32] Requires adequate library size (>10,000 designs) for stable assessment [32]
Distribution Similarity Fréchet ChemNet Distance (FCD) Distance between generated and training molecules in biological/chemical feature space Lower values indicate closer similarity; highly dependent on library size [32]
Distribution Similarity Fréchet Descriptor Distance (FDD) Distance based on physicochemical property distributions Complements FCD; assesses similarity in property space rather than structural space
Goal-Directed Performance Rediscovery Rate Percentage of known active compounds recovered from held-out test set Measures exploitative capability; may favor imitation over innovation
Goal-Directed Performance Multi-parameter Optimization Score Combined score reflecting multiple drug-like properties More realistic but requires careful weighting of parameters

Metrics for Molecular Property Prediction

Table 2: Key Metrics for Molecular Property Prediction Models

Metric Type Specific Metric Application Context Limitations and Considerations
Regression Metrics Root Mean Square Error (RMSE) Continuous properties (e.g., solubility, lipophilicity) Sensitive to outliers; value highly dependent on property range
Regression Metrics Mean Absolute Error (MAE) Continuous properties More robust to outliers than RMSE
Classification Metrics Area Under ROC Curve (AUROC) Binary classification (e.g., target inhibition) May not capture true positive rate relevant for virtual screening [78]
Classification Metrics Precision-Recall AUC Imbalanced datasets More informative than AUROC for skewed class distributions
Classification Metrics Balanced Accuracy Imbalanced datasets Prevents inflation from majority class prediction
Generalization Metrics Inter-scaffold Generalization Performance on structurally novel chemotypes Critical for real-world applicability; measures scaffold hopping ability
Generalization Metrics Intra-scaffold Generalization Performance on analogues of training compounds Measures capability to make accurate predictions within known chemical series
Robustness Metrics Activity Cliff Prediction Accuracy on compounds with small structural changes but large activity differences Particularly challenging for models; significant impact on practical utility [78]

Experimental Protocols and Methodologies

Standardized Evaluation Workflow for Generative Models

G Start Start Evaluation DataPrep Data Preparation and Splitting Start->DataPrep ModelTraining Model Training DataPrep->ModelTraining SplitStrategy SplitStrategy DataPrep->SplitStrategy Time-split vs Random-split Generation Molecule Generation ModelTraining->Generation MetricCalc Metric Calculation Generation->MetricCalc LibSize LibSize Generation->LibSize Library Size ≥10,000 molecules Analysis Result Analysis MetricCalc->Analysis MultiMetric MultiMetric MetricCalc->MultiMetric Multiple Metrics (Table 1) Validation Prospective Validation Analysis->Validation StatRigor StatRigor Analysis->StatRigor Statistical Rigor End Evaluation Complete Validation->End

Evaluation Workflow for Molecular Generative Models

The experimental workflow begins with rigorous data preparation, employing either time-split validation to simulate real-world project progression or random splits for baseline comparison [77]. For model training, chemical language models (CLMs) represent a widely-adopted approach, utilizing architectures such as Recurrent Neural Networks (RNNs), Generative Pretrained Transformers (GPT), and Structured State-Space Sequence models (S4) [32]. A critical implementation detail is the generation of sufficiently large molecular libraries, with evidence indicating that "increasing the number of designs helps avoiding this pitfall" of misleading evaluations [32]. Specifically, libraries should exceed 10,000 designs to ensure metric stability, particularly for distributional similarity measures like FCD. The metric calculation phase should employ the comprehensive set of quantitative indicators outlined in Table 1, while the analysis phase must incorporate statistical rigor through multiple runs with different random seeds to account for inherent variability.

Property Prediction Evaluation Methodology

G Input Molecular Representation RepType Representation Type Input->RepType GNN Graph Neural Networks (GNNs) RepType->GNN Molecular Graph Descriptors Fixed Descriptors (Fingerprints, RDKit2D) RepType->Descriptors Fixed Representation SMILESModel SMILES-Based Models (RNNs, Transformers) RepType->SMILESModel SMILES String EvalFramework Evaluation Framework GNN->EvalFramework Descriptors->EvalFramework SMILESModel->EvalFramework Output Property Prediction EvalFramework->Output CrossVal CrossVal EvalFramework->CrossVal Stratified K-Fold CV EvalMetric EvalMetric EvalFramework->EvalMetric Task-Appropriate Metrics Generalization Generalization EvalFramework->Generalization Generalization Test

Property Prediction Evaluation Methodology

The property prediction evaluation methodology employs multiple molecular representations, each with distinct advantages. Fixed representations including extended-connectivity fingerprints (ECFP) and RDKit2D descriptors provide computationally efficient baselines [78]. Graph Neural Networks (GNNs) process molecular graphs where atoms represent nodes and bonds represent edges, capturing structural relationships without requiring pre-computed descriptors [79]. SMILES-based models, including RNNs and Transformers, process sequential string representations of molecules. The evaluation framework should implement stratified k-fold cross-validation with explicit random seeds to ensure reproducibility and enable meaningful comparison across studies. Recent research indicates that "representation learning models exhibit limited performance in molecular property prediction in most datasets" when compared to traditional fingerprint-based approaches, highlighting the importance of including appropriate baselines [78]. Evaluation must assess both intra-scaffold generalization (predicting properties for analogues of training compounds) and inter-scaffold generalization (predicting properties for novel chemotypes), with the latter being particularly relevant for real-world applications where scaffold hopping is often required.

Table 3: Essential Resources for Molecular AI Research

Resource Category Specific Tool/Resource Application in Validation Technical Specifications
Benchmark Datasets MoleculeNet Standardized benchmark for property prediction Multiple datasets with predefined splits; limited real-world relevance [78]
Benchmark Datasets ChEMBL Public bioactive molecules Large-scale; useful for pretraining but requires careful curation for specific targets [32]
Benchmark Datasets ExCAPE-DB Public bioactivity data Contains temporal information; suitable for time-split validation [77]
Software Libraries RDKit Cheminformatics toolkit Provides molecular descriptors, fingerprints, and standardization functions [78]
Software Libraries Deep Learning Frameworks (PyTorch, TensorFlow) Model implementation Flexible architectures for GNNs, RNNs, and Transformers
Evaluation Metrics MOSES Benchmark for generative models Includes standard metrics (validity, uniqueness, novelty, diversity) [77]
Evaluation Metrics Guacamol Goal-directed generation benchmarks Rediscovery and similarity tasks; may contain analogues in training data [77]
Evaluation Metrics Fréchet ChemNet Distance (FCD) Distribution similarity metric Requires >5,000 molecules per set for stable comparison [32]
Specialized Hardware GPU Clusters Model training and generation Essential for large-scale training and generating sufficient library sizes

Practical Implementation Guidelines for Robust Validation

Addressing the Library Size Pitfall

The library size effect represents a critical validation concern that can fundamentally distort model comparisons. To mitigate this risk, researchers should:

  • Generate large libraries: "Increasing the number of designs" serves as a remedy for the library size pitfall [32]. Libraries should substantially exceed 10,000 designs, with some analyses requiring over 1,000,000 designs for convergence of certain metrics when working with highly diverse training sets [32].

  • Report convergence behavior: Rather than single-point estimates, evaluations should report metric trends across increasing library sizes to demonstrate stability and ensure reported values represent true performance plateaus rather than artifacts of insufficient sampling.

  • Implement scalable metrics: Develop and utilize computationally efficient metrics that remain feasible for large-scale evaluation, as traditional metrics may become prohibitively expensive with library sizes in the millions.

Incorporating Real-World Validation Strategies

Moving beyond academic benchmarks to real-world relevance requires:

  • Time-split validation: Implement time-based splits that mimic realistic project progression by training on early-stage compounds and testing on middle/late-stage compounds [77]. This approach better assesses a model's ability to anticipate future optimization directions rather than merely reconstructing existing knowledge.

  • Multi-parameter optimization assessment: Evaluate models based on their ability to simultaneously optimize multiple properties relevant to drug discovery, reflecting the complex trade-offs required in real-world projects [77].

  • Prospective experimental validation: While resource-intensive, prospective synthesis and testing of generated molecules remains the gold standard for validation [77]. When feasible, even limited prospective validation provides crucial evidence beyond purely computational assessments.

Ensuring Statistical Rigor in Model Evaluation

The field of molecular AI has suffered from insufficient statistical rigor in reporting results. To address this:

  • Multiple random seeds: Perform multiple runs (minimum 5-10) with different random seeds and report mean±standard deviation rather than single-run results to account for variability in training and sampling.

  • Rigorous dataset splitting: Employ stratified splitting methods that maintain similar distributions of key properties across splits, and explicitly report split methodologies to enable fair comparisons and reproducibility.

  • Activity cliff identification: Identify and separately evaluate performance on activity cliffs—pairs of structurally similar compounds with large differences in activity—as these represent particularly challenging cases with significant practical implications [78].

The validation of molecular generative models and property predictors requires a fundamental shift from metric-focused to utility-focused evaluation. This transition necessitates larger library sizes, more realistic dataset splits, multifaceted evaluation criteria, and greater statistical rigor. Within the context of neural state as solution representation in NPDOA research, robust validation frameworks must bridge the gap between retrospective metrics and prospective utility, acknowledging that "evaluating de novo compound design approaches appears, based on the current study, difficult or even impossible to do retrospectively" [77]. By adopting the comprehensive validation strategies outlined in this technical guide, researchers can develop more reliable and clinically translatable AI approaches for biomedicine, ultimately accelerating the journey from algorithmic innovation to therapeutic impact.

Assessing Computational Complexity, Convergence Speed, and Solution Quality

Within the field of meta-heuristic optimization, the Neural Population Dynamics Optimization Algorithm (NPDOA) represents a significant advancement inspired by the computational principles of brain neuroscience [1]. This algorithm conceptualizes potential solutions to optimization problems as neural states within interconnected neural populations, simulating the decision-making and cognitive processes of the human brain [1]. The core thesis of this whitepaper is that the framework of "neural state as solution representation" is not merely a metaphorical construct but a foundational principle that directly governs the performance characteristics of NPDOA, including its computational complexity, convergence speed, and ultimate solution quality. This guide provides an in-depth technical assessment of these performance metrics, offering researchers and practitioners a detailed framework for evaluation and application.

Neural State as Solution Representation: A Foundational Framework

In NPDOA, the traditional representation of a candidate solution is re-envisioned as a dynamic neural state. Each decision variable in a solution vector corresponds to a neuron, and its value represents that neuron's firing rate [1]. This conceptual shift from a static solution point to a dynamic neural state is central to the algorithm's operation and performance.

The algorithm operates by simulating the dynamics of multiple interconnected neural populations through three core strategies [1]:

  • Attractor Trending Strategy: Drives neural populations towards optimal decisions, ensuring exploitation capability.
  • Coupling Disturbance Strategy: Deviates neural populations from attractors via coupling with other populations, improving exploration ability.
  • Information Projection Strategy: Controls communication between neural populations, enabling a transition from exploration to exploitation.

These dynamics create a rich, biologically-plausible mechanism for navigating complex solution spaces, balancing the discovery of promising regions (exploration) with refining the best solutions found (exploitation).

Assessing Computational Complexity

The computational complexity of an algorithm provides a theoretical estimate of the resources it requires, typically expressed as a function of input size. For population-based metaheuristics like NPDOA, the relevant parameters are the population size (N), the dimensionality of the problem (D), and the maximum number of iterations (T).

Theoretical Complexity Analysis

A computational complexity analysis of NPDOA indicates that its time complexity is O(N ⋅ D ⋅ T) [1]. This complexity arises from the main loop of the algorithm, which iterates T times, and within each iteration, updates all D dimensions for all N individuals in the population. This places NPDOA in a similar complexity class as other standard population-based algorithms like Particle Swarm Optimization (PSO) and Genetic Algorithms (GA), making it scalable for high-dimensional optimization problems.

Comparative Complexity of Meta-Heuristic Algorithms

Table 1: Comparative Computational Complexity of Meta-Heuristic Algorithms

Algorithm Acronym Theoretical Time Complexity
Neural Population Dynamics Optimization Algorithm [1] NPDOA O(N ⋅ D ⋅ T)
Particle Swarm Optimization [80] PSO O(N ⋅ D ⋅ T)
Genetic Algorithm [1] GA O(N ⋅ D ⋅ T)
Differential Evolution [1] DE O(N ⋅ D ⋅ T)
Whale Optimization Algorithm [1] WOA O(N ⋅ D ⋅ T)

Evaluating Convergence Speed

Convergence speed measures how quickly an algorithm approaches a solution of satisfactory quality. The neural state dynamics of NPDOA are explicitly designed to accelerate this process.

Mechanisms for Rapid Convergence

The attractor trending strategy directly propels neural states (solutions) towards favorable decisions (good solutions), creating a strong exploitative force that accelerates convergence [1]. Furthermore, the information projection strategy dynamically regulates the interplay between the attractor and coupling strategies, ensuring a smooth and timely transition from global exploration to local refinement, which is critical for avoiding stagnation and maintaining convergence momentum [1].

Experimental Benchmarking

Quantitative evaluations on standard benchmark suites, such as CEC 2017 and CEC 2022, demonstrate NPDOA's competitive convergence performance. The algorithm has been shown to surpass several state-of-the-art metaheuristic algorithms in convergence efficiency [1]. For instance, in a comparative study, a related mathematics-inspired algorithm, the Power Method Algorithm (PMA), achieved superior average Friedman rankings (2.69 for 100 dimensions) compared to other contemporary algorithms [28], highlighting the potential of novel dynamics like those in NPDOA to enhance convergence speed on complex problems.

G Start Initial Neural Population Attractor Attractor Trending Strategy Start->Attractor Coupling Coupling Disturbance Strategy Start->Coupling Projection Information Projection Strategy Attractor->Projection Ensures Exploitation Coupling->Projection Ensures Exploration Update Update Neural States (Solutions) Projection->Update Balances Exploration/Exploitation Update->Attractor Feedback Loop Update->Coupling Feedback Loop Converge Converged Optimal Solution Update->Converge

Diagram 1: The NPDOA's convergence is driven by the interaction of its three core strategies, which dynamically manage neural states to efficiently navigate the solution space.

Quantifying Solution Quality

Solution quality refers to the accuracy, precision, and robustness of the final solution obtained by an algorithm. The "neural state" framework contributes directly to high-quality outcomes through its enhanced exploratory capabilities.

Mechanisms for High-Quality Solutions

The coupling disturbance strategy is critical for maintaining solution quality. By deviating neural populations from their current attractors, it introduces disruptions that help the algorithm escape local optima [1]. This mechanism directly counteracts premature convergence, a common failure mode in optimization, thereby ensuring a more thorough search of the solution space and a higher probability of locating the global optimum or a very high-quality local optimum.

Benchmark and Practical Problem Performance

Empirical validation is crucial. NPDOA's efficacy has been verified through systematic testing on both benchmark functions and practical engineering problems [1]. The results demonstrate that the algorithm offers distinct benefits when addressing many single-objective optimization problems. Its performance has been benchmarked against nine other meta-heuristic algorithms, confirming its ability to achieve competitive and robust solution quality [1].

Table 2: Example Benchmark Performance of a Contemporary Meta-Heuristic Algorithm (Power Method Algorithm) on CEC 2022 [28]

Algorithm Average Friedman Rank (30D) Average Friedman Rank (50D) Average Friedman Rank (100D)
Power Method Algorithm (PMA) 3.00 2.71 2.69
Algorithm B 4.25 4.12 4.35
Algorithm C 5.10 5.33 5.21
Algorithm D 4.95 5.04 4.90

Experimental Protocols for Performance Assessment

A standardized experimental protocol is essential for the fair and reproducible evaluation of NPDOA.

Benchmark Suite Selection
  • Test Functions: Utilize established benchmark suites like CEC 2017 and CEC 2022, which contain a diverse set of unimodal, multimodal, hybrid, and composition functions [28].
  • Practical Engineering Problems: Apply NPDOA to real-world problems such as the compression spring design, cantilever beam design, pressure vessel design, and welded beam design [1]. These problems test the algorithm's performance under real-world constraints.
Experimental Setup and Metrics
  • Implementation: Experiments can be executed using platforms like PlatEMO v4.1 run on a computer with a standard CPU (e.g., Intel Core i7-12700F) and sufficient RAM (e.g., 32 GB) [1].
  • Performance Metrics:
    • Solution Quality: Best, median, and worst objective function value over multiple independent runs.
    • Convergence Speed: Mean number of iterations or function evaluations to reach a predefined accuracy threshold.
    • Robustness: Standard deviation of the final solution quality across multiple runs.
  • Statistical Validation: Employ non-parametric statistical tests like the Wilcoxon rank-sum test for pairwise comparisons and the Friedman test with post-hoc analysis for multiple algorithm comparisons to confirm the significance of performance differences [28].

The Scientist's Toolkit: Research Reagent Solutions

Table 3: Key Computational Tools and Resources for NPDOA Research

Research Reagent Function in Performance Assessment
PlatEMO v4.1 [1] A MATLAB-based platform for experimental evolutionary multi-objective optimization, used for running comparative experiments and generating performance data.
CEC Benchmark Suites [28] Standardized sets of test functions (e.g., CEC 2017, 2022) used to quantitatively evaluate and compare algorithm performance on known problems.
Statistical Test Suites (Wilcoxon, Friedman) [28] Statistical methods used to rigorously determine if performance differences between NPDOA and other algorithms are statistically significant.
Engineering Problem Models [1] Mathematical models of real-world problems (e.g., pressure vessel design) used to validate the practical utility and solution quality of NPDOA.

The framework of "neural state as solution representation" is the cornerstone of the Neural Population Dynamics Optimization Algorithm's performance. This in-depth assessment demonstrates that NPDOA achieves a well-balanced synergy between its core components: its computational complexity is competitive with state-of-the-art metaheuristics, its convergence speed is accelerated by the attractor trending and information projection strategies, and its solution quality is robustly maintained by the coupling disturbance strategy's ability to evade local optima. Empirical results from both benchmark and practical problems confirm that NPDOA is a powerful and promising tool for tackling complex optimization challenges. Future research may focus on extending this neural state paradigm to multi-objective, constrained, and large-scale dynamic optimization problems.

Conclusion

The Neural Population Dynamics Optimization Algorithm (NPDOA) represents a significant leap in bio-inspired computation, effectively translating the brain's decision-making processes into a powerful tool for drug discovery. By representing solutions as neural states and dynamically balancing search strategies, NPDOA demonstrates robust performance in navigating the complex, high-dimensional landscapes of molecular design and target prioritization. While challenges in parameter tuning and problem-specific adaptation remain, its validated success against benchmarks and practical problems underscores its potential. Future directions should focus on hybrid models that integrate NPDOA with Graph Neural Networks for richer molecular representations and its application to personalized medicine frameworks, ultimately accelerating the path from computational prediction to clinical therapy.

References